Trong không gian với hệ trục tọa độ\[Oxyz\], cho điểm \[H\left( {2;1;2} \right)\], \[H\] là hình chiếu vuông góc của gốc tọa độ \[O\] xuống mặt phẳng\[\left( P \right)\]. Tính số đo góc giữa mặt \[\left( P \right)\] và mặt phẳng \[\left( Q \right):x + y - 11 = 0\] theo đơn vị độ.

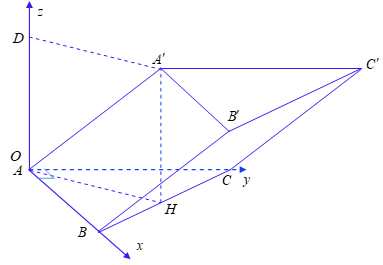
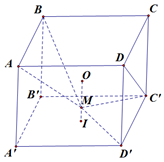
Ta chọn hệ trục tọa độ \(Oxyz\) với \(O \equiv A\) như hình vẽ, chọn \(a = 1\) đơn vị, khi đó ta có tọa độ điểm \(B\left( {1;0;0} \right)\), \(C\left( {0;\sqrt 3 ;0} \right)\) suy ra trung điểm của \(BC\) là \(H\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\), vì \(H\) là hình chiếu của \(A'\) nên suy ra tọa độ của \(A'\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};\sqrt 5 } \right)\). Ta tìm tọa độ \(B'\), gọi tọa độ \(B'\left( {x;y;z} \right)\) khi đó ta có \(\overrightarrow {A'B'}  = \overrightarrow {OB} \) nên tọa độ \(B'\left( {\frac{3}{2};\frac{{\sqrt 3 }}{2};\sqrt 5 } \right)\). Ta cũng có \(\overrightarrow {B'C}  = \left( { - \frac{3}{2};\frac{{\sqrt 3 }}{2}; - \sqrt 5 } \right)\) và \(\overrightarrow {A'B}  = \left( {\frac{1}{2}; - \frac{{\sqrt 3 }}{2}; - \sqrt 5 } \right)\). Từ đó ta có \(\cos \varphi  = \frac{{\left| {\overrightarrow {A'B} .\overrightarrow {B'C} } \right|}}{{\left| {\overrightarrow {A'B} } \right|.\left| {\overrightarrow {B'C} } \right|}}\) \( = \frac{7}{{2.\sqrt 6 .\sqrt 8 }} = \frac{{7\sqrt 3 }}{{24}}\).

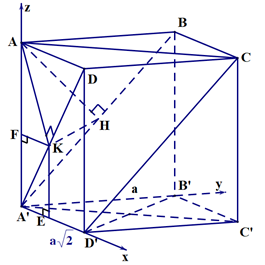
Do \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên \(A'C'\) là hình chiếu vuông góc của \(A'C\) trên $\left(ABCD\right)\Rightarrow (A\text{'}C,(ABCD\left)\right)=(A\text{'}C,A\text{'}C\text{'})=\widehat{CA\text{'}C\text{'}}={30}^0.$

Ta có \(AC = \sqrt {A{B^2} + A{D^2}}  = a\sqrt 3 ;\tan \widehat {CA'C'} = \frac{{CC'}}{{A'C'}} \Rightarrow CC' = a.\)

Kết hợp với giả thiết ta được \(ABB'A'\) là hình vuông và có \(H\) là tâm.

Gọi \(E,F\) lần lượt là hình chiếu vuông góc của \(K\) trên \(A'D'\& A'A.\)

Ta có \(\frac{1}{{A{K^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{A{D^2}}} \Rightarrow AK = \frac{{a\sqrt 6 }}{3};\)\(A'K = \sqrt {A'{A^2} - A{K^2}}  = \frac{a}{{\sqrt 3 }};\)

\(\frac{1}{{K{F^2}}} = \frac{1}{{K{A^2}}} + \frac{1}{{A'{K^2}}} \Rightarrow KF = \frac{{a\sqrt 2 }}{3};KE = \sqrt {A'{K^2} - K{F^2}}  \Rightarrow KE = \frac{a}{3}.\)

Ta chọn hệ trục tọa độ \(Oxyz\) thỏa mãn \(O \equiv A'\) còn \(D',{\rm{ }}B',{\rm{ }}A\) theo thứ tự thuộc các tia \(Ox,{\rm{ }}Oy,{\rm{ }}Oz.\) Khi đó ta có tọa độ các điểm lần lượt là:

\(A(0;0;a),B'(0;a;0),H(0;\frac{a}{2};\frac{a}{2}),K(\frac{{a\sqrt 2 }}{3};0;\frac{a}{3}),E(\frac{{a\sqrt 2 }}{3};0;0),F(0;0;\frac{{a\sqrt 2 }}{3}).\)

Mặt phẳng \(\left( {ABB'A'} \right)\) là mặt phẳng \((yOz)\) nên có VTPT là \({\overrightarrow n _1} = (1;0;0);\)

Ta có \(\left[ {\overrightarrow {AK} ,\overrightarrow {AH} } \right] = \frac{{{a^2}}}{6}{\overrightarrow n _2},{\rm{ }}{\overrightarrow n _2}(2;\sqrt 2 ;\sqrt 2 ).\)

Mặt phẳng \((AKH)\)có VTPT là \({\overrightarrow n _2} = (2;\sqrt 2 ;\sqrt 2 );\)

Gọi \(\alpha \) là góc giữa hai mặt phẳng\(\left( {AHK} \right)\) và \(\left( {ABB'A'} \right)\).