Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SAB\) là tam giác đều và \(\left( {SAB} \right)\) vuông góc với \(\left( {ABCD} \right)\). Tính \(\cos \varphi \) với \(\varphi \) là góc tạp bởi \(\left( {SAC} \right)\) và \(\left( {SCD} \right)\).
Quảng cáo
Trả lời:
Chọn C
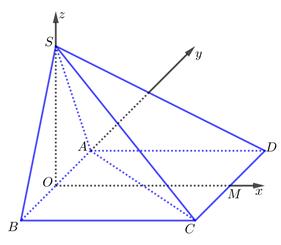
Chú ý: Ta có thể giải bài toán với cạnh hình vuông \[a = 1\].
Gọi \[O,M\] lần lượt là trung điểm của \[AB,CD\]. Vì \[SAB\] là tam giác đều và \[\left( {SAB} \right)\] vuông góc với \[\left( {ABCD} \right)\]nên \[SO \bot \left( {ABCD} \right)\].
Xét hệ trục \[Oxyz\] có \[O\left( {0;0;0} \right),M\left( {1;0;0} \right),A\left( {0;\frac{1}{2};0} \right),S\left( {0;0;\frac{{\sqrt 3 }}{2}} \right)\]. Khi đó \[C\left( {1;\frac{{ - 1}}{2};0} \right),D\left( {1;\frac{1}{2};0} \right)\].
Suy ra \[\overrightarrow {SA} = \left( {0;\frac{1}{2};\frac{{ - \sqrt 3 }}{2}} \right),\overrightarrow {AC} \left( {1; - 1;0} \right),\overrightarrow {SC} = \left( {1;\frac{{ - 1}}{2};\frac{{ - \sqrt 3 }}{2}} \right),\overrightarrow {CD} = \left( {0;1;0} \right)\].
Mặt phẳng \[\left( {SAC} \right)\] có véc tơ pháp tuyến \[\overrightarrow {{n_1}} = \left[ {\overrightarrow {SA} ,\overrightarrow {AC} } \right] = \left( {\frac{{ - \sqrt 3 }}{2};\frac{{ - \sqrt 3 }}{2};\frac{{ - 1}}{2}} \right)\].
Mặt phẳng \[\left( {SAD} \right)\] có véc tơ pháp tuyến \[\overrightarrow {{n_1}} = \left[ {\overrightarrow {SC} ,\overrightarrow {CD} } \right] = \left( {\frac{{\sqrt 3 }}{2};0;1} \right)\].
Vậy \[\cos \varphi = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{5}{7}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
Gọi \(O = AC \cap BD\).
Tam giác \(SAO\) vuông : \(SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{2}\)
Gắn tọa độ như hình vẽ
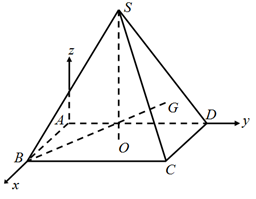
\(A\left( {0;0;0} \right)\), \(B\left( {a;0;0} \right)\), \(C\left( {a;a;0} \right)\), \(D\left( {0;a;0} \right)\), \(O\left( {\frac{a}{2};\frac{a}{2};0} \right)\), \(S\left( {\frac{a}{2};\frac{a}{2};\frac{{a\sqrt 6 }}{2}} \right)\).
Vì \(G\) là trọng tâm tam giác \(SCD\) nên \(G\left( {\frac{a}{2};\frac{{5a}}{6};\frac{{a\sqrt 6 }}{6}} \right)\).
Ta có : \(\overrightarrow {AS} = \left( {\frac{a}{2};\frac{a}{2};\frac{{a\sqrt 6 }}{2}} \right)\) \( = \frac{a}{2}\left( {1;1;\sqrt 6 } \right)\), \(\overrightarrow {BG} = \left( {\frac{{ - a}}{2};\frac{{5a}}{6};\frac{{a\sqrt 6 }}{6}} \right) = \frac{a}{6}\left( { - 3;5;\sqrt 6 } \right)\).
Góc giữa đường thẳng \(BG\) với đường thẳng \(SA\) bằng:
\(\cos \left( {BG;SA} \right) = \frac{{\left| {\overrightarrow {BG} .\overrightarrow {AS} } \right|}}{{BG.AS}}\)\( = \frac{{\left| { - 3 + 5 + 6} \right|}}{{\sqrt {40} .\sqrt 8 }} = \frac{{\sqrt 5 }}{5}\).
Câu 2
Lời giải
Chọn A
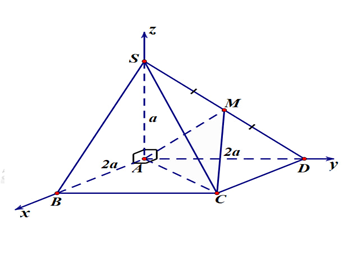
Chọn hệ trục tọa độ sao cho \[A \equiv O\], như hình vẽ:
Khi đó ta có:
\[A\left( {0\,;\,0\,;\,0} \right)\], \[B\left( {2a\,;\,0\,;\,0} \right)\], \[D\left( {0\,;\,2a\,;\,0} \right)\], \[C\left( {2a\,;\,2a\,;\,0} \right)\], \[S\left( {0\,;\,0\,;\,a} \right)\], \[M\left( {0\,;\,a\,;\,\frac{a}{2}} \right)\].
\[\overrightarrow {SB} = \left( {2a\,;\,0\,;\, - a} \right)\],\[\overrightarrow {SC} = \left( {2a\,;\,2a\,;\, - a} \right)\],\[\overrightarrow {MA} = \left( {0\,;\, - a\,;\, - \frac{a}{2}} \right)\],\[\overrightarrow {MC} = \left( {2a\,;\,a\,;\, - \frac{a}{2}} \right)\].
\[\overrightarrow {{n_1}} = \left[ {\overrightarrow {SB} \,,\,\overrightarrow {SC} } \right]\]\[ = \left( {2{a^2}\,;\,0\,;\,4{a^2}} \right)\] và \[\overrightarrow {{n_2}} = \left[ {\overrightarrow {MA} \,,\,\overrightarrow {MC} } \right]\]\[ = \left( {{a^2}\,;\, - {a^2}\,;\,2{a^2}} \right)\].
Gọi \[\alpha \](\(0^\circ \le \alpha \le 90^\circ \)) là góc tạo bởi hai mặt phẳng \[\left( {AMC} \right)\]và \[\left( {SBC} \right)\].
ta có \[cos\alpha = \left| {\cos \left( {\overrightarrow {{n_1}} \,,\,\overrightarrow {{n_2}} } \right)} \right|\]\[ = \frac{{\left| {\overrightarrow {{n_1}} \,.\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|\,.\left| {\overrightarrow {{n_2}} } \right|}}\]
\[ = \frac{{10{a^4}}}{{\sqrt {20.6.{{\left( {{a^4}} \right)}^2}} }}\]\[ = \frac{5}{{\sqrt {30} }}\].
Mà \[{\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} - 1\]\[ = {\left( {\frac{{\sqrt {30} }}{5}} \right)^2} - 1\]\[ = \frac{5}{{25}}\]. Suy ra \[\tan \alpha = \frac{{\sqrt 5 }}{5}\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.