PHẦN II - Câu trắc nghiệm đúng sai:

Một vật có khối lượng 100 g dao động theo phương trình x = 4cos(3πt + 0,5π) (cm).

	Phát biểu	Đúng	Sai
a	Chiều dài quỹ đạo dao động của vật là 8cm
b	Độ lớn vận tốc cực đại của vật là 12π m/s
c	Lấy π2 = 10. Độ lớn gia tốc cực đại của vật là  \(360\left( {{\rm{\;cm}}/{{\rm{s}}^2}} \right)\)
d	Lấy π2 = 10. Độ lớn lực kéo về cực đại tác dụng lên vật là 0,36 N

Hướng dẫn giải

Ta có: \[T = \frac{{2\pi }}{\omega } = 0,5s\]. Mặt khác \[\frac{{\Delta t}}{T} = \frac{{43}}{6} = 7 + \frac{1}{6} \Rightarrow \Delta t = 7T + \frac{T}{6}.\]

Do đó: \[s = 7.4A + \Delta s\]

* Cách 1: Xác định Ds dựa vào vòng tròn:

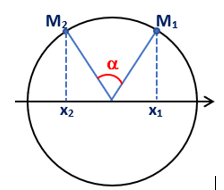
Tại thời điểm ban đầu \[\varphi = \frac{\pi }{3} \Rightarrow x = 2cm\]

Trong thời gian \[\frac{T}{6}\], góc quét trên vòng tròn: \[\alpha = \omega t = \frac{{2\pi }}{T}.\frac{T}{6} = \frac{\pi }{3}\]

® Quét trên vòng tròn, ta thấy vật đến vị trí có li độ \[x = - 2 \Rightarrow \Delta s = 4cm\].

Do đó: s = 28.4 + 4 = 116 cm .

* Cách 2: Xác định Ds dựa vào trục thời gian

Tại thời điểm ban đầu \[\varphi = \frac{\pi }{3} \Rightarrow \left\{ \begin{array}{l}x = 2cm\\v < 0\end{array} \right.\].

Trong thời gian \[\frac{T}{6}\] vật đi từ vị trí có li độ \[x = 2 \to x = - 2 \Rightarrow \Delta s = 4cm\].

Do đó: s = 28.4 + 4 = 116 cm .

Hướng dẫn giải

    a) v_max = ωA = 8π và a_max = ω²A = 16π² → ω = 2π (rad/s

    b) v_max = ωA = 8π và a_max = ω²A = 16π² → ω = 2π (rad/s) và A = 4 (cm)

    c) Tại \(t = 0:x = \frac{A}{2} \oplus \to \varphi = - \frac{\pi }{3}\).

d) Phương trình cần tìm là: x = 4cos\(\left( {2\pi t - \frac{\pi }{3}} \right)\) (cm).