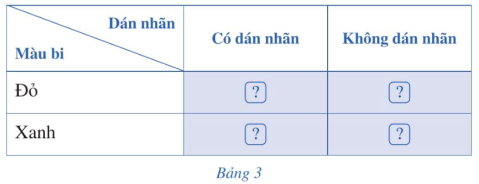
Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6 . Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.
Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6 . Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.
Quảng cáo
Trả lời:
Xét các biến cố:
A: "Chọn được xạ thủ hạng I";
\(B\) : "Viên đạn đó trúng mục tiêu".
Khi đó, \({\rm{P}}(A) = \frac{4}{{10}} = 0,4;{\rm{P}}(\bar A) = \frac{6}{{10}} = 0,6;{\rm{P}}(B\mid A) = 0,75;{\rm{P}}(B\mid \bar A) = 0,6\).
Sơ đồ hình cây biểu thị tình huống đã cho là:
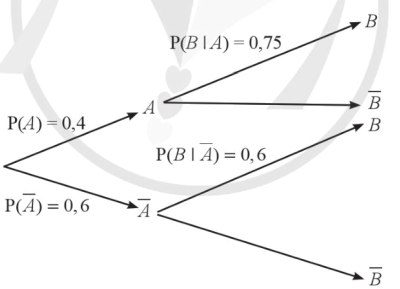
Theo công thức xác suất toàn phần, ta có:
\({\rm{P}}(B) = {\rm{P}}(A) \cdot {\rm{P}}(B\mid A) + {\rm{P}}(\bar A) \cdot {\rm{P}}(B\mid \bar A) = 0,4 \cdot 0,75 + 0,6 \cdot 0,6 = 0,66.{\rm{ }}\)
Vậy xác suất để viên đạn đó trúng mục tiêu là 0,66 .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(A\) là biến cố: "Thứ Ba, ông An đi làm bằng xe máy"; \(B\) là biến cố: "Thứ Tư, ông An đi làm bằng xe máy". Ta cần tính \(P(B)\). Theo công thức xác suất toàn phần, ta có:
\(P(B) = P(A) \cdot P(B\mid A) + P(\bar A) \cdot P(B\mid \bar A).\)
- Tính \(P(A)\) : Vi thứ Hai, ông An đi làm bằng xe buýt nên xác suất để thứ Ba (hôm sau), ông đi làm bằng xe máy là 0,4 . Vậy \(P(A) = 0,4\).
- Tính \(P(\bar A)\) : Ta có \(P(\bar A) = 1 - 0,4 = 0,6\).
- Tính \(P(B\mid A)\) : Đây là xác suất để thứ Tư, ông An đi làm bằng xe máy nếu thứ Ba, ông An đi làm bằng xe máy.
- Theo giả thiết, nếu hôm nay ông đi làm bằng xe máy thì xác suất để hôm sau ông đi làm bằng xe buýt là 0,7 và đi làm bằng xe máy là \(1 - 0,7 = 0,3\). Do đó, nếu thứ Ba , ông An đi làm bằng xe máy thì xác suất để thứ Tư, ông đi làm bằng xe máy là 0,3 . Vậy \(P(B\mid A) = 0,3\).
- Tính \(P(B\mid \bar A)\) : Đây là xác suất để thứ Tư, ông An đi làm bằng xe máy nếu thứ Ba ông An đi làm bằng xe buýt. Theo giả thiết, né́u hôm nay ông đi làm bằng xe buýt thì xác suất để hôm sau ông đi làm bằng xe máy là 0,4 . Do đó nếu thứ Ba, ông An đi làm bằng xe buýt thì
\(P(B) = P(A) \cdot P(B\mid A) + P(\bar A) \cdot P(B\mid \bar A) = 0,4 \cdot 0,3 + 0,6 \cdot 0,4 = 0,36.\)
Lời giải
a) Kí hiệu \(A\) là biến cố: "Thứ Ba, ông An đi làm bằng xe máy"; \(B\) là biến cố: "Thứ Tư, ông An đi làm bằng xe máy".
Ta vẽ sơ đồ hình cây như sau:
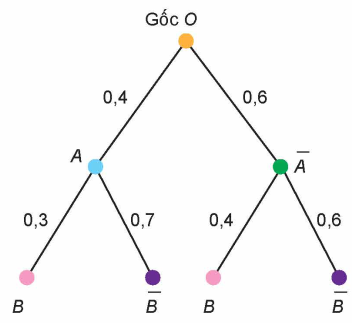
Trên nhánh cây OA và \(O\bar A\) tương ứng ghi \(P(A)\) và \(P(\bar A)\);
Trên nhánh cây AB và \(A\bar B\) tương ứng ghi \(P(B\mid A)\) và \(P(\bar B\mid A)\);
Trên nhánh cây \(\bar AB\) và \(\overline {AB} \) tương ứng ghi \(P(B\mid \bar A)\) và \(P(\bar B\mid \bar A)\).
Có hai nhánh cây đi tới \(B\) là OAB và \(O\bar AB\). Vậy: \(P(B) = 0,4 \cdot 0,3 + 0,6 \cdot 0,4 = 0,36.\)
b) Kí hiệu A là biến cố: "Thứ Ba, ông An đi làm bằng xe máy"; B là biến cố: "Thứ Tư, ông An đi làm bằng xe máy".
Khi đó, biến cố "Thứ Tư, ông An đi làm bằng xe buýt" chính là \(\bar B\).
Ta có sơ đồ hình cây mô tả xác suất của biến cố như sau:
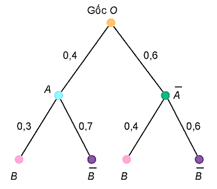
Hai nhánh cây đi tới \(\bar B\) là \(OA\bar B\) và \(O\bar A\bar B\).
Như vậy \(P(\bar B) = 0,4 \cdot 0,7 + 0,6 \cdot 0,6 = 0,64\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.