PHẦN II. TỰ LUẬN
Cho hai vị trí \[A,B\] cách nhau \[615\,{\rm{m}}\], cùng nằm về một phía bờ sông. Khoảng cách từ \[A\] và \[B\] đến bờ sông lần lượt là \[118\,{\rm{m}}\] và \[487\,{\rm{m}}\]. Một người đi từ \[A\] đến bờ sông để lấy nước mang về \[B\]. Xác định độ dài đoạn đường ngắn nhất mà người đó có thể đi.
PHẦN II. TỰ LUẬN
Cho hai vị trí \[A,B\] cách nhau \[615\,{\rm{m}}\], cùng nằm về một phía bờ sông. Khoảng cách từ \[A\] và \[B\] đến bờ sông lần lượt là \[118\,{\rm{m}}\] và \[487\,{\rm{m}}\]. Một người đi từ \[A\] đến bờ sông để lấy nước mang về \[B\]. Xác định độ dài đoạn đường ngắn nhất mà người đó có thể đi.
Quảng cáo
Trả lời:
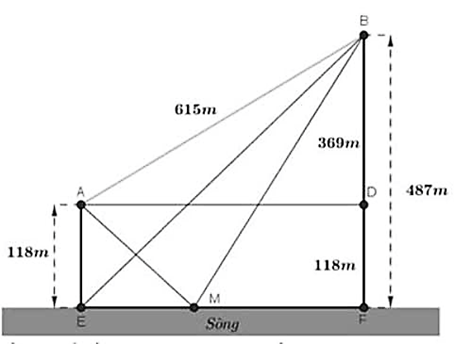
Gọi \[E,F\] là hình chiếu của \[A,B\] trên bờ sông. \[D\] là hình chiếu của \[A\] trên \[BF\].
Áp dụng định lí Pythagore trong tam giác \[ADB\] ta có
\[AD = \sqrt {A{B^2} - B{D^2}} = \sqrt {{{615}^2} - {{\left( {487 - 118} \right)}^2}} = 492\,\,{\rm{m}}\].
Đặt \[EM = x\,\left( {0 \le x \le 492} \right)\] ta có quãng đường mà người đi lấy nước phải đi là
\[S = AM + MB = \sqrt {{{118}^2} + {x^2}} + \sqrt {{{\left( {492 - x} \right)}^2} + {{487}^2}} = \sqrt {{{118}^2} + {x^2}} + \sqrt {{x^2} - 984x + 479233} \].
Ta cần tìm giá trị nhỏ nhất của hàm số \[f\left( x \right) = \sqrt {{{118}^2} + {x^2}} + \sqrt {{x^2} - 984x + 479233} \] trên đoạn \[\left[ {0;492} \right]\].
Cách 1: Sử dụng máy tính dừng chức năng TABLE thu được \[\mathop {{\rm{min}}}\limits_{\left[ {0;492} \right]} f\left( x \right) = 779,8\,{\rm{m}}\].
Cách 2: Ta có \[f'\left( x \right) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} + \frac{{x - 492}}{{\sqrt {{x^2} - 984x + 479233} }}\]
\[f'\left( x \right) = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{x^2} - 984x + 479233} }} \Rightarrow 223245{x^2} + 13701216x - 13924 \cdot 242064 = 0\]
\[ \Rightarrow \left[ \begin{array}{l}x = \frac{{58056}}{{605}}\\x = - \frac{{472}}{3}\;\left( l \right)\end{array} \right. \Rightarrow x = \frac{{58056}}{{605}}\].
Ta có BBT:
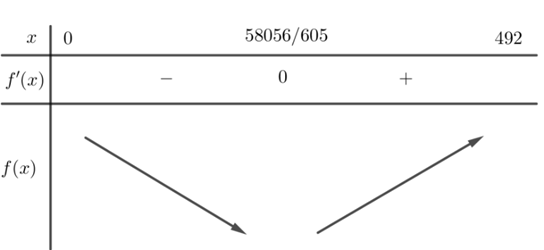
Vậy \[\mathop {{\rm{min}}}\limits_{\left[ {0;492} \right]} f\left( x \right) = f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8\,{\rm{m}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
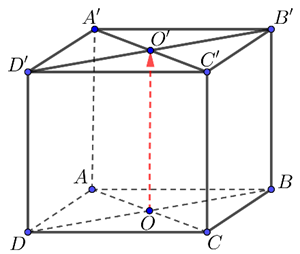
Ta có \(\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} = \left( {\overrightarrow {OA'} + \overrightarrow {OC'} } \right) + \left( {\overrightarrow {OB'} + \overrightarrow {OD'} } \right) = 2\overrightarrow {OO'} + 2\overrightarrow {OO'} = 4\overrightarrow {OO'} \).
Suy ra \(\left| {\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} } \right| = 4\left| {\overrightarrow {OO'} } \right| = 4a\). Chọn A.
Lời giải
Lời giải
Ta có \[y' = 3{x^2} + 2ax + b\].
Đồ thị hàm số đi qua điểm \[\left( {0;2} \right)\]; hàm số có hai điểm cực trị là \[x = 0\] và \[x = 2\], nên ta có hệ phương trình:
\[\left\{ \begin{array}{l}c = 2\\b = 0\\12 + 4a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 0\\c = 2\end{array} \right.\].
Vậy \[a + 2b + 3c = - 3 + 6 = 3\].
Đáp án: 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
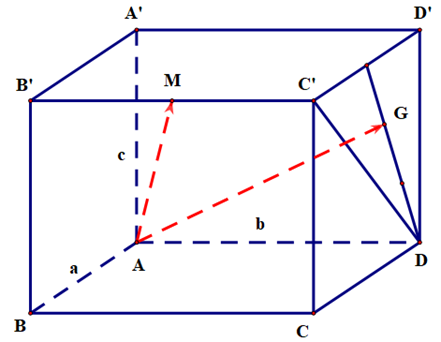
A. \[\overrightarrow {SB} = \overrightarrow {DA} + \overrightarrow {DC} - \overrightarrow {DS} \].
B. \[\overrightarrow {SB} = \overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DS} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số bậc ba \[y = {x^3} + a{x^2} + bx + c\] có đồ thị như hình vẽ dưới đây. Tính giá trị của \[S = a + 2b + 3c\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid11-1756117782.png)
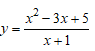 có đồ thị \(\left( C \right)\).
có đồ thị \(\left( C \right)\).