B. TRẮC NGHIỆM ĐÚNG - SAI. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

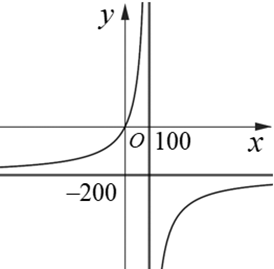
Cho hàm số \(y = f\left( x \right) = \frac{{ - 2x - 3}}{{x + 3}} \cdot \)

a) Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 3; + \infty } \right).\)

b) Đồ thị hàm số có tiệm cận ngang \(y =  - 3.\)

c) Giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ {0;{\rm{ 2025}}} \right]\) là \(f\left( 0 \right)\).

d) Khoảng cách từ tâm đối xứng của đồ thị hàm số đến trục hoành bé hơn \(3.\)

Gọi \[M\left( {{x_0};{y_0}} \right) \in \left( C \right) \Rightarrow M\left( {{x_0};\frac{{x_0^2 + 4{x_0} + 5}}{{{x_0} + 2}}} \right)\].

Gọi \[\left( d \right)\] là khoảng cách từ \[M\] đến đường thẳng \[3x + y + 6 = 0\].

Ta có \[d = \frac{1}{{\sqrt {10} }}\left| {\frac{{4x_0^2 + 16{x_0} + 17}}{{{x_0} + 2}}} \right| = \frac{1}{{\sqrt {10} }}\left| {4\left( {{x_0} + 2} \right) + \frac{1}{{{x_0} + 2}}} \right| \ge \frac{4}{{\sqrt {10} }}\].

Đẳng thức xảy ra \[ \Leftrightarrow 4\left| {{x_0} + 2} \right| = \frac{1}{{\left| {{x_0} + 2} \right|}} \Leftrightarrow \left[ \begin{array}{l}{x_0} = \frac{{ - 3}}{2} \Rightarrow {y_0} = \frac{5}{2}\\{x_0} = \frac{{ - 5}}{2} \Rightarrow {y_0} =  - \frac{5}{2}\end{array} \right.\].

Vậy có hai điểm thoả yêu cầu bài toán là \[{M_1}\left( {\frac{{ - 3}}{2};\frac{5}{2}} \right)\] và \[{M_2}\left( {\frac{{ - 5}}{2};\frac{{ - 5}}{2}} \right)\].

Lời giải

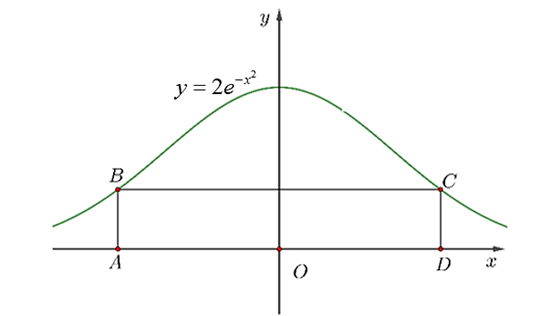
Giả sử điểm \(C\left( {x;2\,{{\rm{e}}^{ - {x^2}}}} \right)\) với \(x > 0\).

Diện tích của hình chữ nhật \(ABCD\) là \(f\left( x \right) = 4x \cdot {{\rm{e}}^{ - {x^2}}}\).

Ta có \(f'\left( x \right) = 4{{\rm{e}}^{ - {x^2}}} - 8{x^2}{{\rm{e}}^{ - {x^2}}}\)\( = 4{{\rm{e}}^{ - {x^2}}}\left( {1 - 2{x^2}} \right)\).

\(f'\left( x \right) = 0\) \( \Rightarrow \left[ \begin{array}{l}x = \frac{{\sqrt 2 }}{2}\,\,\,\,\,\left( n \right)\\x =  - \frac{{\sqrt 2 }}{2}\,\,\,\,\,\,\left( l \right)\end{array} \right.\).

Bảng biến thiên

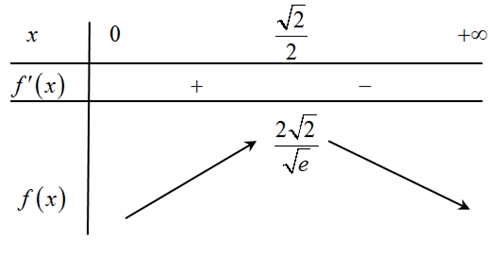
Vậy $\max S_{▭ABCD}=\frac{2\sqrt{2}}{\sqrt{\text{e}}}$.