Trong các biểu thức sau, biểu thức nào luôn nhận giá trị dương:
Quảng cáo
Trả lời:
Lời giải
Đáp án đúng là: C
Xét các đáp án, ta có:
• \(A = {x^2} - x - 6 = {x^2} - 2 \cdot \frac{1}{2}x + {\left( {\frac{1}{2}} \right)^2} - 6 - {\left( {\frac{1}{2}} \right)^2} = {\left( {x - \frac{1}{2}} \right)^2} - \frac{{25}}{4}\).
Nhận thấy \({\left( {x - \frac{1}{2}} \right)^2} - \frac{{25}}{4} \ge - \frac{{25}}{4}\) hay \(A\) đạt giá trị nhỏ nhất bằng \( - \frac{{25}}{4}\).
Do đó, đáp án A loại.
• \(B = {x^2} + x - 2 = {x^2} + 2 \cdot \frac{1}{2}x + {\left( {\frac{1}{2}} \right)^2} - 2 - {\left( {\frac{1}{2}} \right)^2} = {\left( {x + \frac{1}{2}} \right)^2} - \frac{9}{4}\).
Nhận thấy \({\left( {x + \frac{1}{2}} \right)^2} - \frac{9}{4} \ge - \frac{9}{4}\) hay \(B\) đạt giá trị nhỏ nhất bằng \( - \frac{9}{4}\).
Do đó, đáp án B loại.
• \(C = {x^2} - x + 1 = {x^2} - 2 \cdot \frac{1}{2}x + {\left( {\frac{1}{2}} \right)^2} + 1 - {\left( {\frac{1}{2}} \right)^2} = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4}\).
Nhận thấy \({\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge \frac{3}{4}\) hay \(C\) đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\).
Do đó, đáp án C là đúng.
• \(D = {x^2} + 6x - 1 = {x^2} + 2 \cdot 3x + {3^2} - 1 - {3^2} = {\left( {x + 3} \right)^2} - 10\).
Nhận thấy \({\left( {x + 3} \right)^2} - 10 \ge - 10\) hay \(D\) đạt giá trị nhỏ nhất bằng \( - 10\).
Do đó, đáp án D loại.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Đúng
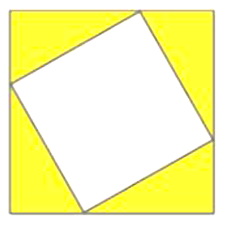
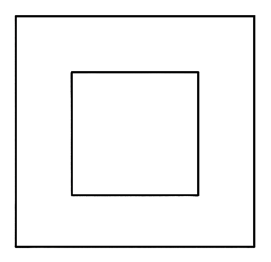
Chu vi hình vuông nhỏ là \(4x\) cm.
Chu vi hình vuông lớn là \(4y\) cm.
Tổng chiều dài các thành kim loại làm khung là 168 cm nên \(4x + 4y = 168\).
b) Sai
Đa thức biểu diện phần diện tích không gắn ảnh (màu vàng) là \(S = {y^2} - {x^2}\) (cm2).
Mà diện tích phần không gắn ảnh là 252 cm2 nên ta có: \({y^2} - {x^2} = 252\).
c) Sai
Ta có: \(4x + 4y = 168\) hay \(4\left( {x + y} \right) = 168\) suy ra \(x + y = 42\).
Có \({y^2} - {x^2} = 252\) hay \(\left( {y - x} \right)\left( {y + x} \right) = 252\) suy ra \(42\left( {y - x} \right) = 252\) nên \(y - x = 6\).
Do đó, \(y = 6 + x\). Thay vào \(x + y = 42\), ta được:
\(x + x + 6 = 42\) hay \(2x = 36\), do đó \(x = 18\) (cm).
Suy ra độ dài cạnh của hình vuông lớn là \(y = 18 + 6 = 24\) (cm).
d) Đúng
Diện tích hình vuông nhỏ chính là diện tích phần gắn ảnh.
Do đó, diện tích phần gắn ảnh là \({18^2} = 324\) (cm2).
Lời giải
Lời giải
a) Đúng
Chiều rộng của thửa ruộng hình chữ nhật này là \(\frac{1}{2}.20 = 10\) (m).
Diện tích của thửa ruộng hình chữ nhật đó là: \(10 \cdot 20 = 200\) (m2).
b) Đúng
Chiều dài của thửa ruộng sau khi giảm \(x{\rm{ }}\left( {\rm{m}} \right)\) là \(20 - x{\rm{ }}\left( {\rm{m}} \right)\).
Chiều rộng của thửa ruộng sau khi tăng \(x{\rm{ }}\left( {\rm{m}} \right)\) là \(10 + x{\rm{ }}\left( {\rm{m}} \right)\).
Do đó, diện tích của thửa ruộng sau khi thay đổi chiều dài, chiều rộng là \(\left( {20 - x} \right)\left( {10 + x} \right){\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
c) Đúng
Nhận thấy, \(S = \left( {20 - x} \right)\left( {10 + x} \right) = - {x^2} + 10x + 200 = - {\left( {x - 5} \right)^2} + 225\).
Nhận thấy \( - {\left( {x - 5} \right)^2} + 225 \le 225\) với mọi \(x\) hay giá trị lớn nhất của \(S = 225{\rm{ }}\left( {{{\rm{m}}^2}} \right)\)
d) Sai
Từ trên, nhận thấy diện tích thửa ruộng đạt giá trị lớn nhất bằng \(225{\rm{ }}\left( {{{\rm{m}}^2}} \right)\) khi \( - {\left( {x - 5} \right)^2} = 0\).
Suy ra \(x = 5.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \({\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} = 4ab.\)
B. \({\left( {a + b} \right)^2} + {\left( {a - b} \right)^2} = 2\left( {{a^2} + {b^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.