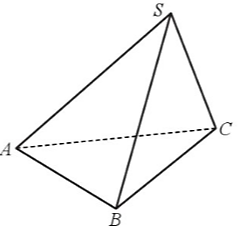
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = 1\) và \(BC = \sqrt 2 \).
a) \(\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {SC} \).
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = \sqrt 2 \).
c) \(\overrightarrow {SC} \cdot \overrightarrow {AB} = \frac{1}{2}\).
d) \(\cos \left( {\overrightarrow {SC} ,\,\overrightarrow {AB} } \right) = \frac{1}{2}\).
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = 1\) và \(BC = \sqrt 2 \).

a) \(\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {SC} \).
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = \sqrt 2 \).
c) \(\overrightarrow {SC} \cdot \overrightarrow {AB} = \frac{1}{2}\).
d) \(\cos \left( {\overrightarrow {SC} ,\,\overrightarrow {AB} } \right) = \frac{1}{2}\).
Quảng cáo
Trả lời:
a) Đúng. Theo quy tắc ba điểm, ta có: \(\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {SB} + \overrightarrow {BC} = \overrightarrow {SC} \).
b) Sai. Ta có \(\left| {\overrightarrow {SA} } \right| = SA = 1;\,\,\left| {\overrightarrow {AB} } \right| = AB = 1;\,\,\left| {\overrightarrow {BC} } \right| = BC = \sqrt 2 \).
c) Sai. Từ giả thiết, ta thấy tam giác \(ABC\) vuông tại \(A\) và tam giác \(SAB\) đều.
Do đó, \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 0\) và \(\left( {\overrightarrow {SA} ,\,\overrightarrow {AB} } \right) = 180^\circ - \widehat {SAB} = 120^\circ \).
Ta có: \[\overrightarrow {SC} \cdot \overrightarrow {AB} = \left( {\overrightarrow {SA} + \overrightarrow {AC} } \right) \cdot \overrightarrow {AB} = \overrightarrow {SA} \cdot \overrightarrow {AB} + \overrightarrow {AC} \cdot \overrightarrow {AB} \]
\( = \overrightarrow {SA} \cdot \overrightarrow {AB} = \left| {\overrightarrow {SA} } \right| \cdot \left| {\overrightarrow {AB} } \right| \cdot \cos 120^\circ = - \frac{1}{2}\).
d) Sai. Ta có: \(\cos \left( {\overrightarrow {SC} ,\,\overrightarrow {AB} } \right) = \frac{{\overrightarrow {SC} \cdot \,\overrightarrow {AB} }}{{\left| {\overrightarrow {SC} } \right| \cdot \,\left| {\overrightarrow {AB} } \right|}} = \frac{{ - \frac{1}{2}}}{{1 \cdot 1}} = - \frac{1}{2}\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
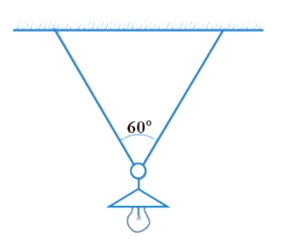
Ta có \(\overrightarrow P = m\overrightarrow g \) nên \(P = \left| {\overrightarrow P } \right| = m \cdot \left| {\overrightarrow g } \right| = 10\) (N).
Bóng đèn ở vị trí cân bằng nên \(\overrightarrow P + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow 0 \) hay \(\overrightarrow P = - \overrightarrow {T'} \) với \(\overrightarrow {T'} = \overrightarrow {{T_1}} + \overrightarrow {{T_2}} \).
Suy ra \(T' = P = 10\,{\rm{N}}\). Vì \({T_1} = {T_2}\) và \(\left( {\overrightarrow {{T_1}} ,\,\overrightarrow {{T_2}} } \right) = 60^\circ \) nên
\(\frac{{T'}}{2} = {T_1} \cdot \cos 30^\circ \Rightarrow {T_1} = \frac{{10}}{{\sqrt 3 }} = \frac{{10\sqrt 3 }}{3}\) (N).
Vậy lực căng của mỗi nửa sợi dây là \(\frac{{10\sqrt 3 }}{3}\,{\rm{N}}\).
Lời giải
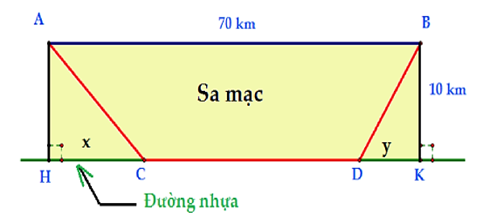
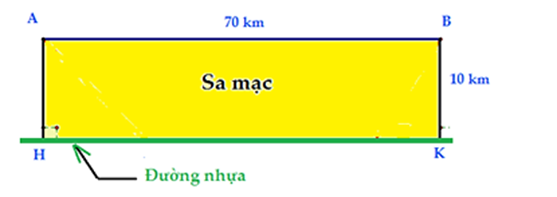
Thời gian nếu đi trực tiếp từ A đến B trên sa mạc là \(\frac{{70}}{{30}} = \frac{7}{3} > 2\).
Do đó, nhà địa chất học không thể đến đúng thời gian quy định.
Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn: \(A \to C \to D \to B\).
Đặt \(HC = x\,\,\left( {0 < x < 70} \right);DK = y\,\,\left( {0 < y < 70} \right)\).
Thời gian đi từ \(A \to C\) là \(\frac{{\sqrt {{{10}^2} + {x^2}} }}{{30}}\).
Thời gian đi từ \(C \to D\) là \(\frac{{70 - \left( {x + y} \right)}}{{50}}\).
Thời gian đi từ \(D \to B\) là \(\frac{{\sqrt {{{10}^2} + {y^2}} }}{{30}}\).
Tổng thời gian đi từ \(A \to B\) theo cách này là:
\(\frac{{\sqrt {{{10}^2} + {x^2}} }}{{30}} + \frac{{70 - \left( {x + y} \right)}}{{50}} + \frac{{\sqrt {{{10}^2} + {y^2}} }}{{30}} = \frac{{\sqrt {{{10}^2} + {x^2}} }}{{30}} + \frac{{35 - x}}{{50}} + \frac{{\sqrt {{{10}^2} + {y^2}} }}{{30}} + \frac{{35 - y}}{{50}} = f\left( x \right) + f\left( y \right)\).
Xét \(f\left( u \right) = \frac{{\sqrt {{{10}^2} + {u^2}} }}{{30}} + \frac{{35 - u}}{{50}}\), \(0 < u < 70\).
Ta có \(f'\left( u \right) = \frac{u}{{30\sqrt {{{10}^2} + {u^2}} }} - \frac{1}{{50}};f'\left( u \right) = 0 \Rightarrow u = \frac{{15}}{2}\).
Lập bảng biến thiên ta được \(\mathop {\min }\limits_{u \in \left( {0;70} \right)} f\left( u \right) = f\left( {\frac{{15}}{2}} \right) = \frac{{29}}{{30}}\).
Khi đó \(f\left( x \right) + f\left( y \right) \ge \frac{{29}}{{30}} + \frac{{29}}{{30}} = \frac{{29}}{{15}} \approx 1,93\).
Dấu “=” xảy ra khi \(x = y = \frac{{15}}{2}\).
Vậy để đến B sớm nhất thì ông ta phải đi trên đoạn AC một khoảng 12,5 km, đoạn CD một khoảng 45 km và đi trên đoạn DB một khoảng 12,5 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
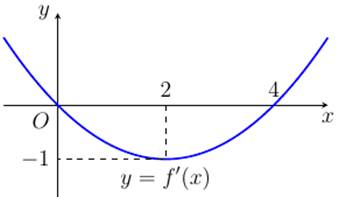
A. \(\left( {1;2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.