Bộ 5 đề thi giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 3
37 người thi tuần này 4.6 1.4 K lượt thi 21 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
Lời giải
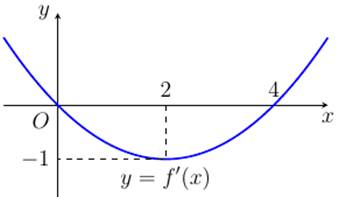
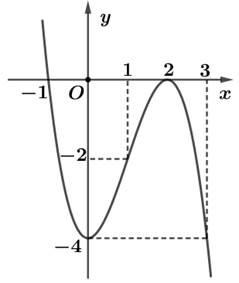
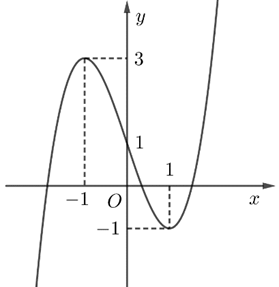
Từ đồ thị hàm số ta thấy hàm số \(y = f\left( x \right)\) đồng biến khoảng \(\left( {0\,;\,2} \right)\). Vậy hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;1} \right)\). Chọn D.
Câu 2
D. -1.
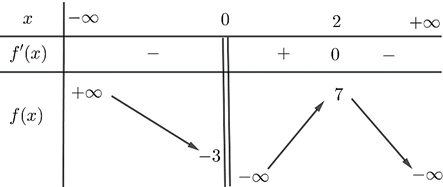
Lời giải
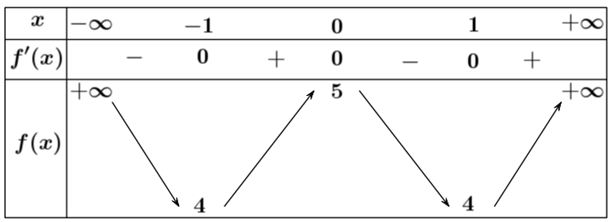
Từ bảng biến thiên ta thấy giá trị cực đại của hàm số bằng 5. Chọn B.
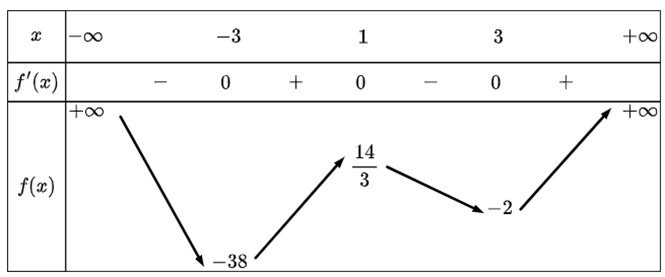
Câu 3
Lời giải
Từ bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 10;10} \right]\) là \( - 38\) tại \[x = - 3\].
Chọn B.
Câu 4
Lời giải
Đồ thị hàm số đã cho có đường tiệm cận đứng là \(x = - \frac{1}{3}\). Chọn D.
Câu 5
Lời giải
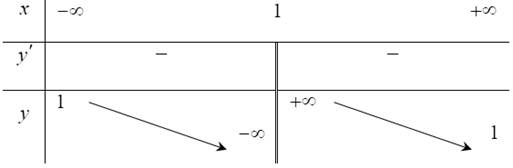
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2 - x}}{{2x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{x} - 1}}{{2 + \frac{1}{x}}} = - \frac{1}{2}\); \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2 - x}}{{2x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\frac{2}{x} - 1}}{{2 + \frac{1}{x}}} = - \frac{1}{2}\).
Nên tiệm cận ngang của đồ thị hàm số \(y = \frac{{2 - x}}{{2x + 1}}\) là \(y = - \frac{1}{2}\). Chọn C.
Câu 6
A. \(\left( { - 1;\;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
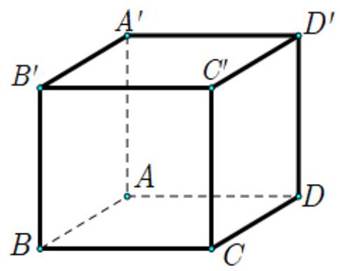
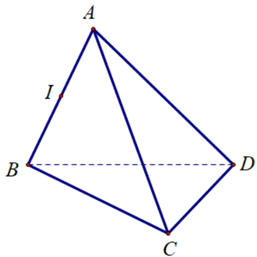
Câu 8
A. \(\overrightarrow {CD} \).
B. \(\overrightarrow {AB} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\left( {1;2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Title: 20241022132335314 - Description: \begin{tikzpicture}[scale=.7, font=\footnotesize, line join=round, line cap=round, >=stealth]
\def\bc{4} % cạnh BC
\def\ba{2} % cạnh BA
\def\gocB{35} % góc B của đáy
\coordinate[label=below left:$B$] (B) at (0,0);
\coordinate[label=above left:$A$] (A) at (\gocB:\ba);
\coordinate[label=below:$C$] (C) at (\bc,0);
\coordinate[label=right:$D$] (D) at ($(C)-(B)+(A)$);
\coordinate[label=above left:$A'$] (A') at ($(A)+(90:\bc)$);
\coordinate[label=left:$B'$] (B') at ($(B)-(A)+(A')$);
\coordinate[label=below right:$C'$] (C') at ($(C)-(A)+(A')$);
\coordinate[label=right:$D'$] (D') at ($(D)-(A)+(A')$);
\draw (B')--(B)--(C)--(D)--(D')--(A')--(B')--(C')--(D') (C)--(C');
\draw[dashed] (A')--(A)--(D) (A)--(B);
\foreach \diem in {A,B,C,D,A',B',C',D'} \fill (\diem)circle(1.5pt);
\end{tikzpicture}](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid58-1756388228.png)