Trong không gian Oxyz, cho hai điểm A(1; 3; 1), B(1; −2; 3). Biết điểm M(x; 0; z) thuộc mặt phẳng tọa độ (Oxz) sao cho MA + MB ngắn nhất. Tính giá trị của biểu thức P = 3z – x2.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có 2 điểm A, B nằm khác phía với mặt phẳng (Oxz).
Khi đó MA + MB AB.
Dấu “=” xảy ra khi M là giao điểm của AB với mặt phẳng (Oxz).
Suy ra \(\overrightarrow {AM} ,\overrightarrow {AB} \) cùng phương và M (Oxz).
Giả sử M(x; y; z).
Có \(\overrightarrow {AB} = \left( {0; - 5;2} \right),\overrightarrow {AM} = \left( {x - 1;y - 3;z - 1} \right)\).
Suy ra \(\left\{ \begin{array}{l}x - 1 = 0\\y - 3 = - 5k\\z - 1 = 2k\\y = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\k = \frac{3}{5}\\z = \frac{{11}}{5}\\y = 0\end{array} \right.\)\( \Rightarrow M\left( {1;0;\frac{{11}}{5}} \right)\).
Do đó \(P = 3z - {x^2} = 3.\frac{{11}}{5} - {1^2} = 5,6\).
Trả lời: 5,6.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
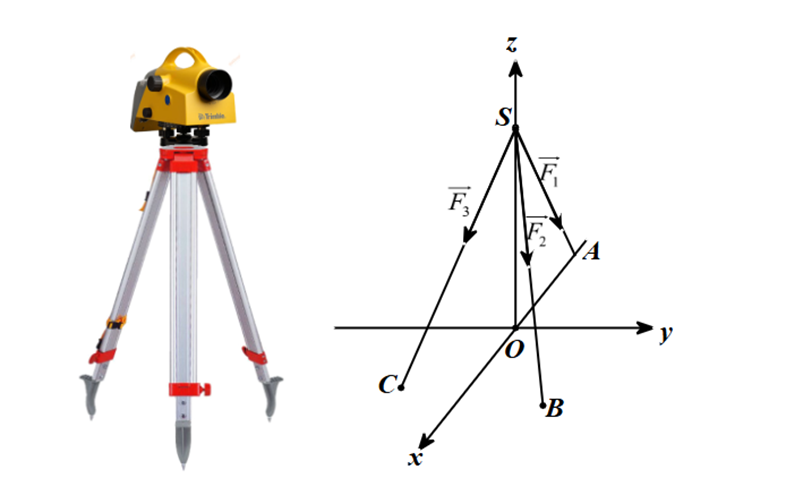
Ta có \(\overrightarrow {SA} = \left( { - 2;0; - 4} \right),\overrightarrow {SB} = \left( {1;\sqrt 3 ; - 4} \right),\overrightarrow {SC} = \left( {1; - \sqrt 3 ; - 4} \right)\)\( \Rightarrow SA = SB = SC = \sqrt {20} \).
Lại có \(\overrightarrow {AB} = \left( {3;\sqrt 3 ;0} \right),\overrightarrow {AC} = \left( {3; - \sqrt 3 ;0} \right),\overrightarrow {BC} = \left( {0; - 2\sqrt 3 ;0} \right)\)\( \Rightarrow AB = AC = BC = \sqrt {12} \).
Do đó hình chóp S.ABC đều có đường cao là SO = 4 với O(0; 0; 0) là trọng tâm tam giác ABC.
Mặt khác, \(\overrightarrow {{F_1}} = k\overrightarrow {SA} = \left( { - 2k;0; - 4k} \right),\overrightarrow {{F_2}} = k\overrightarrow {SB} = \left( {k;\sqrt 3 k; - 4k} \right),\overrightarrow {{F_3}} = k\overrightarrow {SC} = \left( {k; - \sqrt 3 k; - 4k} \right)\)
\( \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \left( {0;0; - 12k} \right)\).
Mà \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P = \left( {0;0; - 30} \right)\) nên \( - 12k = - 30 \Leftrightarrow k = \frac{5}{2}\).
Suy ra \(\overrightarrow {{F_1}} = \left( { - 5;0; - 10} \right),\overrightarrow {{F_2}} = \left( {\frac{5}{2};\frac{{5\sqrt 3 }}{2}; - 10} \right)\).
Vậy \(\overrightarrow {{F_1}} .\overrightarrow {{F_2}} = \frac{{175}}{2} = 87,5\).
Trả lời: 87,5.
Lời giải
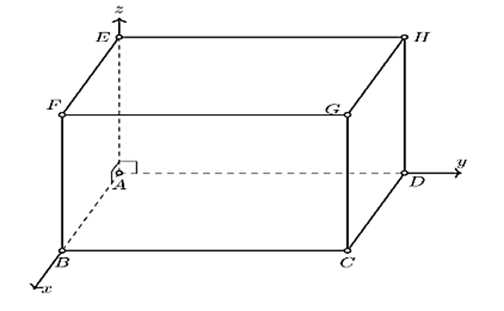
Theo đề ta có A(0; 0; 0), B(6; 0; 0), D(0; 7; 0), E(0; 0; 5).
Vì K là tâm của ABCD nên K là trung điểm của BD. Suy ra K(3; 3,5; 0).
H (Oyz) H(0; 7; 5).
Vì N là trọng tâm của tam giác AHK nên \(\left\{ \begin{array}{l}a = \frac{{0 + 3 + 0}}{3} = 1\\b = \frac{{0 + 3,5 + 7}}{3} = \frac{7}{2}\\c = \frac{{0 + 0 + 5}}{3} = \frac{5}{3}\end{array} \right.\).
Do đó P = 2a – 4b + 3c \( = 2.1 - 4.\frac{7}{2} + 3.\frac{5}{3} = - 7\).
Trả lời: −7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.
\(M(0;0; - 3)\).
B.
\(M( - 8; - 4;7)\).
C.
\(M(8;{\mkern 1mu} {\mkern 1mu} 4; - 7)\).
D.
\(M\left( {0;0;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo