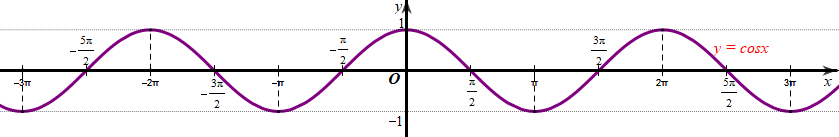Một bệnh nhân hàng ngày phải uống một viên thuốc \(150\,{\rm{mg}}\). Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn \(5\% \). Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
Một bệnh nhân hàng ngày phải uống một viên thuốc \(150\,{\rm{mg}}\). Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn \(5\% \). Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày đầu tiên là \(150\,{\rm{mg}}\).
Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn \(5\% \).
Do đó, lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ hai là
\(150 + 150 \cdot 5\% = 150\left( {1 + 0,05} \right)\) (mg).
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ ba là
\(150 + 150\left( {1 + 0,05} \right) \cdot 5\% = 150 + 150\left( {0,05 + 0,{{05}^2}} \right) = 150\left( {1 + 0,05 + 0,{{05}^2}} \right)\) (mg).
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ tư là
\(150 + 150\left( {1 + 0,05 + 0,{{05}^2}} \right) \cdot 5\% = 150\left( {1 + 0,05 + 0,{{05}^2} + 0,{{05}^3}} \right)\) (mg).
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ năm là
\(150 + 150\left( {1 + 0,05 + 0,{{05}^2} + 0,{{05}^3}} \right) \cdot 5\% = 150\left( {1 + 0,05 + 0,{{05}^2} + 0,{{05}^3} + 0,{{05}^4}} \right)\)\( = 157,8946875\,\,{\rm{(mg)}}.\)
Cứ tiếp tục như vậy, ta ước tính lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong một thời gian dài là
\(S = 150\left( {1 + 0,05 + 0,{{05}^2} + 0,{{05}^3} + 0,{{05}^4} + \ldots } \right)\) (mg).
Nhận thấy rằng \(0,05 + 0,{05^2} + 0,{05^3} + 0,{05^4} + \ldots \) là tổng của một cấp số nhân lùi vô hạn với số hạng đầu \({u_1} = 0,05\) và công bội \(q = 0,05\).
Do đó, \(1 + 0,05 + 0,{05^2} + 0,{05^3} + 0,{05^4} + \ldots = 1 + \frac{{{u_1}}}{{1 - q}} = 1 + \frac{{0,05}}{{1 - 0,05}} = \frac{{20}}{{19}}\).
Suy ra \(S = 150 \cdot \frac{{20}}{{19}} = \frac{{3000}}{{19}}\).
Vậy lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài ước tính khoảng \(\frac{{3000}}{{19}}\) mg.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét \({u_{n + 1}} - {u_n} = \frac{{m\left( {n + 1} \right) - 1}}{{\left( {n + 1} \right) + 1}} - \frac{{mn - 1}}{{n + 1}} = \frac{{mn + m - 1}}{{n + 2}} - \frac{{mn - 1}}{{n + 1}}\)
\( = \frac{{m{n^2} + 2mn + m - n - 1 - \left( {m{n^2} + 2mn - n - 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{{m + 1}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\).
Dãy số đã cho là dãy giảm \( \Leftrightarrow {u_{n + 1}} - {u_n} < 0 \Leftrightarrow \frac{{m + 1}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} < 0,\forall n \in {\mathbb{N}^*} \Leftrightarrow m < - 1\)
\(\left( {{\rm{do }}\left( {n + 2} \right)\left( {n + 1} \right) > 0,\forall n \in {\mathbb{N}^*}} \right){\rm{. }}\)
Với \(m\) là số nguyên lớn nhất và \(m < - 1\) suy ra \(m = - 2\).
Đáp án: −2.
Câu 2
A. \({u_n} = \frac{1}{n}\).
B. \({u_n} = 3n\).
C. \({u_n} = {2^n} + 1\).
D. \({u_n} = {2^n}\).
Lời giải
¨ Dãy số \({u_n} = \frac{1}{n}\) có \[{u_1} = 1;{u_2} = \frac{1}{2};{u_3} = \frac{1}{3};...\] nên \(\frac{{{u_2}}}{{{u_1}}} \ne \frac{{{u_3}}}{{{u_2}}}\), do đó không phải là cấp số nhân.
¨ Dãy số \({u_n} = 3n\) có \[{u_1} = 3;{u_2} = 6;{u_3} = 9;...\] nên \(\frac{{{u_2}}}{{{u_1}}} \ne \frac{{{u_3}}}{{{u_2}}}\), do đó không phải là cấp số nhân.
¨ Dãy số \({u_n} = {2^n} + 1\) có \[{u_1} = 3;{u_2} = 5;{u_3} = 9;...\] nên \(\frac{{{u_2}}}{{{u_1}}} \ne \frac{{{u_3}}}{{{u_2}}}\), do đó không phải là cấp số nhân.
¨ Dãy số \({u_n} = {2^n}\) có \[\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{{2^{n + 1}}}}{{{2^n}}} = 2\] không đổi với mọi n, nên đây là cấp số nhân với công bội \[q = 2\].
Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left( {0;\pi } \right)\).
B. \(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
C. \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
D. \(\left( { - 3\pi ; - 2\pi } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \( - \frac{1}{3}.\)
B. \(\frac{2}{3}.\)
C. \( - \frac{2}{3}.\)
D. \(\frac{1}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo