Cho tứ diện \(ABCD\), gọi \(G\) và \(E\) lần lượt là trọng tâm của tam giác \(ABD\) và \(ABC\). Mệnh đề nào dưới đây đúng?
\(GE\)và \(CD\) chéo nhau.
\(GE{\rm{//}}CD\).
\(GE\)và \(AD\)cắt nhau.
\(GE\)và \(CD\)cắt nhau.
Quảng cáo
Trả lời:
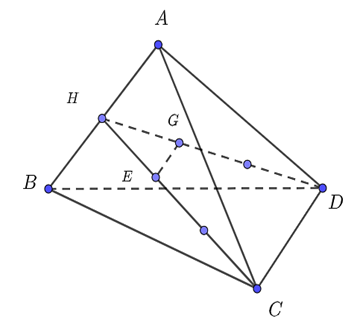
Gọi \(H\) là trung điểm \(AB\). Khi đó \(G\) và \(E\) lần lượt là trọng tâm của tam giác \(ABD\) và \(ABC\) nên \[\frac{{HG}}{{HD}} = \frac{{HE}}{{HC}} = \frac{1}{3}\]. Suy ra \(GE{\rm{//}}CD\). Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \[ - a + b \le h\left( t \right) = a\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + b \le a + b,\forall t\].
Theo bài ra: \[\left\{ \begin{array}{l}a + b = 114,5\\ - a + b = 0,5\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}a = 57\\b = 57,5\end{array} \right.\].
Suy ra \[h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\].
b) Cabin \(M\) đạt được chiều cao \(86\) m khi \[h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5 = 86\]
\[ \Leftrightarrow \sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}\frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{\pi }{6} + k2\pi \\\frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 5 + 15k\\t = 10 + 15k\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right).\]
Vậy trong vòng quay đầu tiên cabin \(M\) đạt được chiều cao \(86\) m tại thời điểm \(t = 5\) phút hoặc \(t = 10\) phút.
Lời giải
Gọi \(n\left( {n \in {\mathbb{N}^*}} \right)\)là số ngày mỗi học sinh nuôi heo đất để số tiền đạt được là \[5658800\] đồng.
Vì lớp 11A có tất cả 43 học sinh nên mỗi học sinh sau n ngày đều có số tiền nuôi heo đất là:
\[\frac{{5658800}}{{43}} = 131600\] đồng.
Ngày đầu tiên mỗi bạn nuôi heo \[2000\] đồng, từ ngày thứ hai trở đi mỗi bạn nuôi heo hơn ngày liền trước là \[200\] đồng, do đó số tiền nuôi heo của mỗi bạn mỗi ngày trong n ngày lập thành một cấp số cộng \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} = 2000\) và công sai \(d = 200\).
Ta có \({S_n} = {u_1} + {u_2} + .... + {u_n} = \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right) \cdot d} \right] = 131600\)
\[ \Leftrightarrow \frac{n}{2}\left[ {4000 + \left( {n - 1} \right) \cdot 200} \right] = 131600 \Leftrightarrow 100{n^2} + 1900n - 131600 = 0\].
Giải phương trình ta được \(n = 28\)(loại đi \(n = - 47\)vì \(n \in {\mathbb{N}^*}\)).
Vậy sau \(28\)ngày thì số tiền nuôi heo đất của lớp 11A thu được là \[5658800\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.