Một công ty dịch vụ cho thuê xe hơi vào dịp Tết với giá thuê mỗi chiếc xe hơi như sau: khách thuê tối thiểu phải thuê trọn ba ngày Tết (mùng \(1,2,3\)) với giá 1 triệu đồng/ngày; những ngày còn lại (nếu khách còn thuê) sẽ được tính giá thuê là 700 000 đồng/ngày. Giả sử \(T\) là tổng số tiền mà khách phải trả khi thuê một chiếc xe hơi của công ty và \(x\) là số ngày thuê của khách.
a) Hàm số \(T\) theo \(x\) là \(T = 900\,000 + 700\,000x\).
b) Điều kiện của \(x\) là \(x \in \mathbb{N}\).
c) Một khách hàng thuê một chiếc xe hơi công ty trong 7 ngày tết thì sẽ trả khoản tiền thuê là \(5\,800\,000\)(đồng).
d) Anh Bình định dành ra một khoản tối đa là 10 triệu đồng cho phí thuê xe đi chơi trong dịp tết, khi đó anh Bình có thể thuê xe của công ty trên tối đa 12 ngày.
Một công ty dịch vụ cho thuê xe hơi vào dịp Tết với giá thuê mỗi chiếc xe hơi như sau: khách thuê tối thiểu phải thuê trọn ba ngày Tết (mùng \(1,2,3\)) với giá 1 triệu đồng/ngày; những ngày còn lại (nếu khách còn thuê) sẽ được tính giá thuê là 700 000 đồng/ngày. Giả sử \(T\) là tổng số tiền mà khách phải trả khi thuê một chiếc xe hơi của công ty và \(x\) là số ngày thuê của khách.
a) Hàm số \(T\) theo \(x\) là \(T = 900\,000 + 700\,000x\).
b) Điều kiện của \(x\) là \(x \in \mathbb{N}\).
c) Một khách hàng thuê một chiếc xe hơi công ty trong 7 ngày tết thì sẽ trả khoản tiền thuê là \(5\,800\,000\)(đồng).
d) Anh Bình định dành ra một khoản tối đa là 10 triệu đồng cho phí thuê xe đi chơi trong dịp tết, khi đó anh Bình có thể thuê xe của công ty trên tối đa 12 ngày.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng. Ta có \(T = 3\,000\,000 + 700\,000\left( {x - 3} \right) = 900\,000 + 700\,000x\) (đồng) với điều kiện \(x \ge 3,x \in \mathbb{N}\).
b) Sai. Theo câu a), ta có điều kiện của \(x\) là \(x \ge 3,x \in \mathbb{N}\).
c) Đúng. Với \(x = 7\) thì \(T = 900\,000 + 700\,000 \cdot 7 = 5\,800\,000\) (đồng).
d) Sai. Xét bất phương trình
\[900\,000 + 700\,000x \le 10\,000\,000 \Leftrightarrow 9 + 7x \le 100 \Leftrightarrow x \le \frac{{91}}{7} = 13.\]
Vậy với khoản tiền 10 triệu đồng, anh Bình có thể thuê một chiếc xe tối đa 13 ngày.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Kí hiệu \(A\) là tập hợp học sinh tham gia tiết mục nhảy Flashmob, \(B\) là tập hợp học sinh tham gia tiết mục hát, \(E\) là tập hợp học sinh trong lớp. Ta có thể biểu diễn ba tập hợp đó bằng biểu đồ Ven như hình sau:
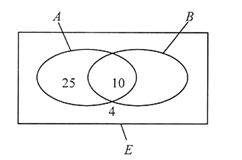
Khi đó, \(A \cap B\) là tập hợp học sinh tham gia cả hai tiêt mục. Số phần tử của tập hợp \(A\) là 35 , số phần tử của tập hợp \(A \cap B\) là 10 , số phần tử của tập hợp \(E\) là 45 .
Số học sinh tham gia ít nhất một trong hai tiết mục là \(45 - 4 = 41\) (học sinh).
Số học sinh tham gia tiết mục hát mà không tham gia tiết mục nhảy Flashmob là \(41 - 35 = 6\) (học sinh).
Số học sinh tham gia tiết mục hát là \(6 + 10 = 16\) (học sinh).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
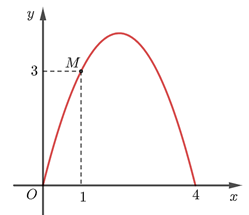
Cổng dạng parabol có thể xem là đồ thị của hàm số bậc hai: \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) \(\left( P \right)\).
Theo bài ra ta có \(\left( P \right)\) đi qua 3 điểm sau: \(O\left( {0\,;\,0} \right),\,M\left( {1\,;\,3} \right),\,N\left( {4\,;\,0} \right)\).
Suy ra ta có hệ phương trình sau: \(\left\{ \begin{array}{l}c = 0\\a + b + c = 3\\16a + 4b + c = 0\end{array} \right.\) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}c = 0\\a = - 1\\b = 4\end{array} \right.\).
Vậy parabol \(\left( P \right)\) có phương trình là: \(y = - {x^2} + 4x\). Parabol \(\left( P \right)\) có đỉnh là \(D\left( {2\,;\,4} \right)\).
Chiều cao của cổng là tung độ đỉnh của parabol \(\left( P \right)\):\(y = - {x^2} + 4x\).
Vậy chiều cao của cổng là 4 mét.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập