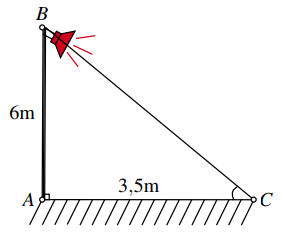
Một cột đèn \(AB\) cao 6 m có bóng in trên mặt đất là \(AC\) dài \(3,5\;{\rm{m}}\). Góc (làm tròn đến phút) mà tia sáng từ đèn \(B\) tạo với mặt đất là

Tìm số tự nhiên \(x\) nhỏ nhất thỏa mãn bất phương trình \[3 < \frac{{2x - 2}}{8}\].

Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)

Cho phương trình \[x + 2y = 3.\]

a) Cặp số \[\left( {5;\,\, - 1} \right)\] là một nghiệm của phương trình đã cho.

b) Phương trình đã cho là phương trình bậc nhất một ẩn.

c) Tất cả nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \(y = 3 - \frac{1}{2}x.\)

d) Phương trình đã cho có vô số nghiệm, nghiệm tổng quát là \(\left( {3 - 2y;\,\,y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

(0,5 điểm) Người ta dùng 100 m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của mảnh vườn là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được.

Cho phương trình \[\left( {x - 2} \right)\left( {3x + 5} \right) = \left( {2x - 4} \right)\left( {x + 1} \right)\]. Hỏi có bao nhiêu giá trị của \(x\) thỏa mãn phương trình đã cho?