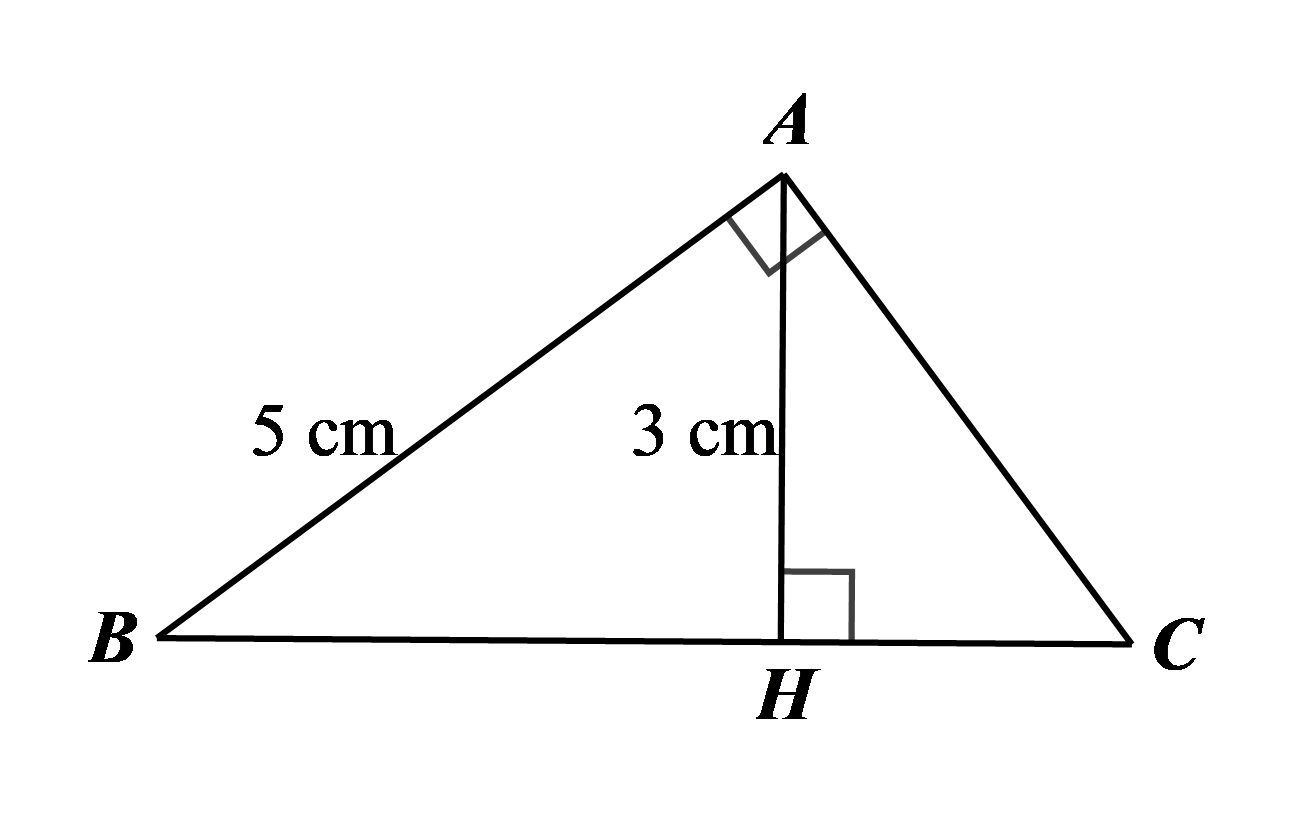Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 5{\rm{\;cm}}\) và đường cao \(AH = 3{\rm{\;cm}}.\) Tính số đo góc \(C\) (làm tròn kết quả đến độ).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 5{\rm{\;cm}}\) và đường cao \(AH = 3{\rm{\;cm}}.\) Tính số đo góc \(C\) (làm tròn kết quả đến độ).
Quảng cáo
Trả lời:
|
Hướng dẫn giải Đáp số: \(53.\) Xét \(\Delta ABH\) vuông tại \(H,\) ta có: \[\sin B = \frac{{AH}}{{AB}} = \frac{3}{5}.\] Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(\widehat {B\,} + \widehat {C\,} = 90^\circ \), suy ra \(\cos C = \sin B = \frac{3}{5}.\) |
|
Sử dụng MTCT, ta bấm lần lượt các phím:
Trên màn hình cho kết quả \(53^\circ 7'48.37'',\) làm tròn đến phút ta được \(53^\circ .\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: 14.
Ta có \[3 < \frac{{2x - 2}}{8}\]
\[2x - 2 > 24\]
\[2x > 26\]
\[x > 26:2\]
\[x > 13.\]
Do đó, bất phương trình có nghiệm \[x > 13.\]
Vậy số tự nhiên nhỏ nhất của \(x\) thỏa mãn bất phương trình đã cho là \[x = 14.\]
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\)
\(\frac{2}{3}x + 6 = 0\) hoặc \(8 - 2x = 0\)
\(\frac{2}{3}x = - 6\) hoặc \(2x = 8\)
\(x = - 9\) hoặc \(x = 4\)
Vậy phương trình đã cho có hai nghiệm là \(x = - 9\,;\) \(x = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.