Cho hình bình hành \(ABCD.\) Nếu \(\widehat A = 90^\circ \) thì:
A. \(AC = \frac{1}{2}BD.\)
Quảng cáo
Trả lời:
Đáp án đúng là: D
Hình bình hành \(ABCD\) có \(\widehat A = 90^\circ \) nên \(ABCD\) là hình chữ nhật. Do đó, \(AC = BD.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(5\)
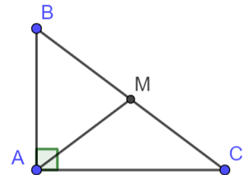
Vì chu vi tam giác \(ABC\) bằng \(24\;{\rm{cm}}\)nên \(AB + BC + AC = 24\;\left( {{\rm{cm}}} \right).\)
Vì \(AB:AC:BC = 3:4:5\) nên \(\frac{{AB}}{3} = \frac{{AC}}{4} = \frac{{BC}}{5}.\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AB}}{3} = \frac{{AC}}{4} = \frac{{BC}}{5} = \frac{{AB + AC + BC}}{{3 + 4 + 5}} = \frac{{24}}{{12}} = 2.\)
Do đó, \(BC = 2 \cdot 5 = 10\;\left( {{\rm{cm}}} \right).\)
Vì tam giác \(ABC\) vuông tại \(A.\)
Mà \(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên \(AM = \frac{1}{2}BC = \frac{1}{2} \cdot 10 = 5\;\left( {{\rm{cm}}} \right).\)
Vậy \(AM = 5\;{\rm{cm}}{\rm{.}}\)
Lời giải
Đáp án: \(5\)
Vì chu vi hình chữ nhật \(ABCD\) bằng \(14\;{\rm{cm}}\) nên \(2\left( {DC + AD} \right) = 14\;{\rm{cm}}\) nên \(AD + DC = 7\;{\rm{cm}}{\rm{.}}\)
Vì chu vi tam giác \(ACD\) bằng \(12\;{\rm{cm}}\) nên \(DC + AD + AC = 12\;\left( {{\rm{cm}}} \right).\)
Do đó, \(7 + AC = 12\) hay \(AC = 5\;{\rm{cm}}{\rm{.}}\)
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(BD = AC = 5\;{\rm{cm}}{\rm{.}}\) Vậy \(BD = 5\;{\rm{cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.