Một khung dây dẫn kín có 100 vòng, mỗi vòng có diện tích 50 cm$^2$, được đặt trong từ trường đều có độ lớn cảm ứng từ 0,4 T. Cho khung dây quay đều quanh trục $\Delta$ ($\Delta$ nằm trong mặt phẳng khung dây và vuông góc với vectơ cảm ứng từ) với tốc độ 12 vòng/giây. Điện trở của khung dây là 1,6 $\Omega$. Chọn gốc thời gian $t=0$ là thời điểm vectơ cảm ứng từ cùng phương, cùng chiều với vectơ đơn vị pháp tuyến của mặt phẳng khung dây. Biểu thức cường độ dòng điện chạy trong khung dây dẫn kín là
Một khung dây dẫn kín có 100 vòng, mỗi vòng có diện tích 50 cm$^2$, được đặt trong từ trường đều có độ lớn cảm ứng từ 0,4 T. Cho khung dây quay đều quanh trục $\Delta$ ($\Delta$ nằm trong mặt phẳng khung dây và vuông góc với vectơ cảm ứng từ) với tốc độ 12 vòng/giây. Điện trở của khung dây là 1,6 $\Omega$. Chọn gốc thời gian $t=0$ là thời điểm vectơ cảm ứng từ cùng phương, cùng chiều với vectơ đơn vị pháp tuyến của mặt phẳng khung dây. Biểu thức cường độ dòng điện chạy trong khung dây dẫn kín là
A. $i = 1{,}5.\cos\!\left(24\pi t - \dfrac{\pi}{2}\right)\ \text{A.}$
B. $i = 3\pi.\sin\!\left(12\pi t - \dfrac{\pi}{2}\right)\ \text{A.}$
C. $i = 1{,}5.\sin\!\left(12\pi t - \dfrac{\pi}{2}\right)\ \text{A.}$
Quảng cáo
Trả lời:
Đáp án đúng là D
Khung dây dẫn kín quay đều với tốc độ góc là: $\ \omega = 2\pi f = 2\pi.12 = 24\pi\ \text{rad/s}$
Tại thời điểm ban đầu $t=0$, ta có $\vec{B}$ cùng hướng với $\vec{n}$ hay $(\vec{B};\vec{n})=\varphi=0\ \text{rad.}$
Biểu thức của từ thông qua khung dây là:
$\displaystyle \Phi = NBS\cos(\varphi+\omega t) = 100.0{,}4.50.10^{-4}.\cos(24\pi t)=0{,}2.\cos(24\pi t)\ \text{(Wb).}$
Biểu thức suất điện động cảm ứng trong khung dây là:}
$\displaystyle e_c = -\dfrac{d\Phi}{dt} = 0{,}2.24\pi.\sin(24\pi t) = 4{,}8\pi.\cos\!\left(24\pi t-\dfrac{\pi}{2}\right)\ \text{(V).}$
Biểu thức cường độ dòng điện chạy trong khung dây dẫn kín đó là:}
$\displaystyle i=\dfrac{e_c}{R}=\dfrac{4{,}8\pi.\cos\!\left(24\pi t-\dfrac{\pi}{2}\right)}{1{,}6}=3\pi.\cos\!\left(24\pi t-\dfrac{\pi}{2}\right)\ \text{(A).}$
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. $\dfrac{13}{2} nRT$
B. $\dfrac{11}{2} nRT$
C. $\dfrac{9}{2} nRT$
Lời giải
Đáp án đúng là A
Quá trình (1)→(2) là đẳng tích, nên
\[
\frac{p_1}{T_1}=\frac{p_2}{T_2}\ \Rightarrow\ \frac{p_0}{T}=\frac{2p_0}{T_2}\ \Rightarrow\ T_2=2T,
\]
và khối khí không thực hiện công nên \(A_{12}=0\).
Quá trình (2)→(3) là đẳng áp, nên
\[
\frac{V_2}{T_2}=\frac{V_3}{T_3}\ \Rightarrow\ \frac{V_0}{2T}=\frac{2V_0}{T_3}\ \Rightarrow\ T_3=4T.
\]
Công do khối khí thực hiện:
\[
A_{23}=p_2\Delta V=p_2\,(V_3-V_2)=2p_0V_0.
\]
Từ phương trình trạng thái tại (1): \(p_0V_0=nRT\Rightarrow A_{23}=2nRT\).
Nội năng của khí (đơn nguyên tử) \(U=\tfrac{3}{2}nRT\), do đó
\[
U_1=\tfrac{3}{2}nRT,\qquad
U_2=\tfrac{3}{2}nRT_2=\tfrac{3}{2}nR(2T)=3nRT,\qquad
U_3=\tfrac{3}{2}nRT_3=\tfrac{3}{2}nR(4T)=6nRT.
\]
Độ biến thiên nội năng và nhiệt lượng từng đoạn:
\[
\Delta U_{12}=U_2-U_1=3nRT-\tfrac{3}{2}nRT=\tfrac{3}{2}nRT,
\]
\[
\Delta U_{12}=A_{12}+Q_{12}\Rightarrow Q_{12}=\tfrac{3}{2}nRT.
\]
Với quy ước \(A>0\) là công do ngoài thực hiện lên khí, đoạn (2)→(3) khí nở làm công ra ngoài nên \(A_{23}=-2nRT\). Khi đó
\[
\Delta U_{23}=U_3-U_2=6nRT-3nRT=3nRT=A_{23}+Q_{23}
\Rightarrow Q_{23}=3nRT-(-2nRT)=5nRT.
\]
Tổng nhiệt lượng khí nhận trong (1)→(2)→(3) là
\[
Q=Q_{12}+Q_{23}=\tfrac{3}{2}nRT+5nRT=\tfrac{13}{2}\,nRT.
\]
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
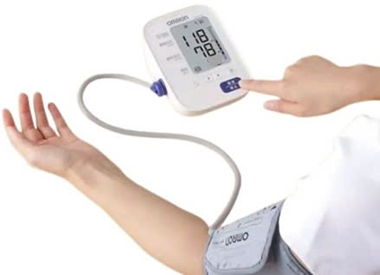
Áp suất của khối khí trong vòng bít đạt giá trị nhỏ nhất và lớn nhất trong quá trình đo lần lượt là $760 \,\text{mmHg}$ và $920 \,\text{mmHg}$.
|
Đ |
|
|
b |
Nếu không khí được bơm liên tục vào vòng bít thì để độ chênh lệch giữa áp suất khí trong vòng bít và áp suất khí quyển từ $0 \,\text{mmHg}$ đến $160 \,\text{mmHg}$ ta cần bơm khí trong $9 \,\text{s}$. |
|
S |
|
c |
Lượng không khí đã được bơm vào vòng bít để độ chênh lệch giữa áp suất khí trong vòng bít và áp suất khí quyển tăng từ $0 \,\text{mmHg}$ đến $160 \,\text{mmHg}$ xấp xỉ bằng $0,014 \,\text{mol}$.
|
Đ |
|
|
d |
d & Động năng tịnh tiến trung bình của các phân tử khí trong vòng bít trước khi bơm không khí vào xấp xỉ bằng $6,21 \cdot 10^{-21} \,\text{J}$.
|
Đ |
|
a) ĐÚNG
Áp suất khí trong vòng bít lúc bắt đầu bơm là:
\[
p_1 = \Delta p_1 + p_0 = 0 + 760 = 760 \,\text{mmHg}.
\]
Áp suất khí trong vòng bít khi độ chênh lệch giữa áp suất khí trong vòng bít và áp suất khí quyển đạt giá trị lớn nhất là:
\[
p_2 = \Delta p_2 + p_0 = 160 + 760 = 920 \,\text{mmHg}.
\]
Vậy áp suất của khối khí trong vòng bít đạt giá trị nhỏ nhất và lớn nhất trong quá trình đo lần lượt là $760 \,\text{mmHg}$ và $920 \,\text{mmHg}$.
b) SAI
Trong quá trình bơm, nhiệt độ khí không đổi nên ta có:
\[
p_1 V_1 = p_2 V_2 \;\;\Rightarrow\;\; 760 \cdot (120 + 30t) = 920 \cdot 380
\]
\[
\Rightarrow t = \frac{34}{3} \approx 11 \,\text{s}.
\]
c) ĐÚNG
Áp dụng phương trình Clapeyron cho khối khí trong vòng bít tại thời điểm có độ chênh lệch giữa áp suất khí trong vòng bít và áp suất khí quyển bằng $0 \,\text{mmHg}$ và bằng $160 \,\text{mmHg}$ lần lượt ta có:
\[
p_1 V_0 = n_1 R T \quad \Rightarrow \quad n_1 = \frac{p_1 V_0}{R T} = \frac{101325 \cdot 120 \cdot 10^{-6}}{8,31 \cdot (27+273)} \approx 0,0055 \,\text{mol}.
\]
\[
p_2 V_2 = n_2 R T \quad \Rightarrow \quad n_2 = \frac{p_2 V_2}{R T} = \frac{122025 \cdot 380 \cdot 10^{-6}}{8,31 \cdot (27+273)} \approx 0,0195 \,\text{mol}.
\]
Lượng không khí đã được bơm vào vòng bít để độ chênh lệch giữa áp suất khí trong vòng bít và áp suất khí quyển tăng từ $0 \,\text{mmHg}$ đến $160 \,\text{mmHg}$ là:
\[
\Delta n = n_2 - n_1 = 0,0195 - 0,0055 \approx 0,014 \,\text{mol}.
\]
d) ĐÚNG
Động năng tịnh tiến trung bình của phân tử khí trong vòng bít trước khi bơm không khí vào là:
\[
W_\text{đ} = \frac{3}{2} k T = \frac{3}{2} \cdot 1,38 \cdot 10^{-23} \cdot (27 + 273) \approx 6,21 \cdot 10^{-21} \,\text{J}.
\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
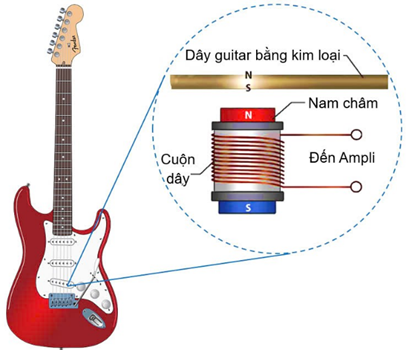
A. Khi gảy đàn, đoạn dây gần nam châm điện bị nhiễm từ dao động và tạo ra sự biến thiên từ thông qua cuộn dây.
B. Trong cuộn dây xuất hiện suất điện động cảm ứng khi gảy đàn. Tín hiệu điện được đưa đến bộ khuếch đại và loa tạo ra sóng âm.
C. Nam châm vĩnh cửu có vai trò góp phần làm tăng suất điện động cảm ứng gấp nhiều lần.
D. Bộ cảm ứng trong ghita điện hoạt động dựa trên hiện tượng cảm ứng điện từ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. $47^\circ\mathrm{C}$
B. $48^\circ\mathrm{C}$
C. $53^\circ\mathrm{C}$
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.