Trong một cuộc tập luyện chạy Marathon, người ta ước tính “nữ hoàng chân đất” Phạm Thị Bình của Việt Nam tiêu tốn khoảng $E = 2{,}52 \times 10^6$ calo (cal). Giả sử có 40\% năng lượng tiêu tốn được dùng cho vận động, phần năng lượng còn lại chuyển thành nhiệt thải ra ngoài nhờ sự bay hơi của nước qua hô hấp và da để giữ cho nhiệt độ cơ thể của cô không đổi. Coi nhiệt độ cơ thể của cô không đổi và nhiệt hoá hơi riêng của nước ở nhiệt độ cơ thể của cô thể hiện là $L = 2{,}4 \times 10^6\,\text{J/kg}$. Lấy $1$ cal = $4{,}18$ J. Khối lượng riêng của nước là $D = 1{,}0 \times 10^3\,\text{kg/m}^3$.

Phần năng lượng chuyển thành nhiệt thải cho cuộc tập luyện này là $x \times 10^6$ J. Tìm $x$ (làm tròn kết quả đến chữ số hàng phần trăm).
Trong một cuộc tập luyện chạy Marathon, người ta ước tính “nữ hoàng chân đất” Phạm Thị Bình của Việt Nam tiêu tốn khoảng $E = 2{,}52 \times 10^6$ calo (cal). Giả sử có 40\% năng lượng tiêu tốn được dùng cho vận động, phần năng lượng còn lại chuyển thành nhiệt thải ra ngoài nhờ sự bay hơi của nước qua hô hấp và da để giữ cho nhiệt độ cơ thể của cô không đổi. Coi nhiệt độ cơ thể của cô không đổi và nhiệt hoá hơi riêng của nước ở nhiệt độ cơ thể của cô thể hiện là $L = 2{,}4 \times 10^6\,\text{J/kg}$. Lấy $1$ cal = $4{,}18$ J. Khối lượng riêng của nước là $D = 1{,}0 \times 10^3\,\text{kg/m}^3$.

Phần năng lượng chuyển thành nhiệt thải cho cuộc tập luyện này là $x \times 10^6$ J. Tìm $x$ (làm tròn kết quả đến chữ số hàng phần trăm).
Quảng cáo
Trả lời:
Phần năng lượng chuyển thành nhiệt thải là
\[
Q = HE = 60\% \cdot 2{,}52 \times 10^6 \cdot 4{,}18 = 6{,}32 \times 10^6\,J
\]
\[
\Rightarrow x = 6{,}32
\]
Câu hỏi cùng đoạn
Câu 2:
Hỏi có khoảng bao nhiêu lít nước đã thoát ra ngoài cơ thể của cô cho cuộc tập luyện này (làm tròn kết quả đến chữ số hàng phần trăm)?
Hỏi có khoảng bao nhiêu lít nước đã thoát ra ngoài cơ thể của cô cho cuộc tập luyện này (làm tròn kết quả đến chữ số hàng phần trăm)?
Khối lượng nước đã bay hơi là
\[
m = \frac{Q}{L} = \frac{6{,}32 \times 10^6}{2{,}4 \times 10^6} \approx 2{,}63\,\text{kg}.
\]
Thể tích nước đã thoát ra ngoài cơ thể là
\[
V = \frac{m}{D} = \frac{2{,}63}{1{,}0 \times 10^3} \approx 2{,}63 \times 10^{-3}\,\text{m}^3 = 2{,}63\,\text{lít}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Với sai số dưới 10%, nhiệt độ tuyệt đối của lượng khí tăng bao nhiêu lần thì áp suất của nó tăng bấy nhiêu lần. |
Đ |
|
|
b |
Lượng khí đã dùng trong thí nghiệm là . |
|
S |
|
c |
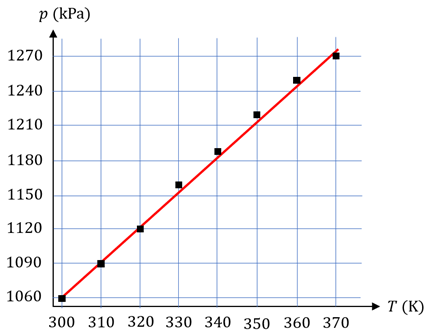
Đồ thị biểu diễn mối liên hệ giữa và có dạng như hình vẽ. |
Đ |
|
|
d |
Lấy tỉ số giữa (tính theo đơn vị kPa) và (tính theo đơn vị K) với hai chữ số có nghĩa, khi nhiệt độ tuyệt đối của lượng khí là thì áp suất của nó bằng . |
|
S |
a) Ta tính được tỉ số $\dfrac{p}{T}$ (kPa/K) cho từng lần đo như bảng sau đây:

Ta thấy: với sai số dưới 10\% thì $\dfrac{p}{T} \approx 3{,}5 \,\text{(kPa/K)}$ trong 7 lần đo, chỉ có lần đo 8 mới có $\dfrac{p}{T} \approx 3{,}4 \,\text{(kPa/K)}$. Do đó ta có thể nói $T$ tăng bao nhiêu lần thì $p$ tăng bấy nhiêu lần, tức là $p$ tỉ lệ thuận với $T$.
b) Giá trị trung bình của tỉ số $\dfrac{p}{T}$ trong tất cả các lần đo với hai chữ số có nghĩa là $3{,}5 \,\text{(kPa/K)}$.
Dùng phương trình Clapeyron ta tính được số mol của lượng khí này là:
\[
n = \frac{pV}{RT} = \frac{p}{T} \cdot \frac{V}{R} = 3{,}5 \cdot 10^3 \cdot \frac{25 \cdot 10^{-6}}{8{,}31} \approx 10{,}5 \cdot 10^{-3} \,\text{mol} \approx 11 \cdot 10^{-3} \,\text{mol}.
\]
c) Đồ thị biểu diễn mối liên hệ giữa $p$ và $T$ có dạng như hình trên là chính xác.
d) Lấy tỉ số giữa $p$ (tính theo đơn vị kPa) và $T$ (tính theo đơn vị K) với hai chữ số có nghĩa thì ta có $\dfrac{p}{T} \approx 3{,}5 \,\text{(kPa/K)}$. Do đó khi lượng khí có nhiệt độ tuyệt đối là $285$ K thì áp suất của nó là:
\[
p = 3{,}5 \cdot 285 = 997{,}5\, \text{kPa} \approx 998\,\text{kPa}.
\]
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Lực điện mà hạt nhân của nguyên tử hydrogen tác dụng lên electron là lực hút và có độ lớn |
Đ |
|
|
b |
Tốc độ chuyển động của electron là $v = 2{,}2 \times 10^6 \,\text{m/s}$.
|
Đ |
|
|
c |
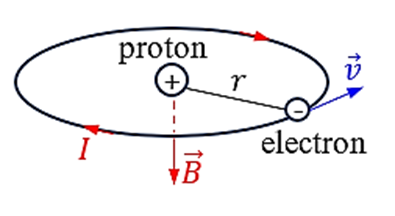
Sự chuyển động của electron quanh hạt nhân tạo nên một dòng điện tròn có cường độ $I = 1\,\text{A}$. |
|
S |
|
d |
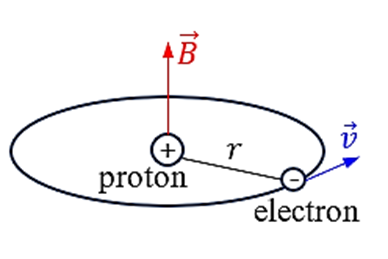
Cảm ứng từ do dòng điện tròn nói trên gây ra tại hạt nhân của nguyên tử hydrogen có chiều như hình vẽ và có độ lớn $B = 4{,}0\,\text{T}$.
|
|
S |
a) Lực điện mà hạt nhân của nguyên tử hydrogen tác dụng lên electron là lực hút vì chúng có điện tích trái dấu và có độ lớn
\[
F = k \frac{e^2}{r^2} = 9 \cdot 10^9 \cdot \frac{(1{,}6 \times 10^{-19})^2}{(5{,}3 \times 10^{-11})^2} \approx 8{,}2 \times 10^{-8}\,N
\]
b) Lực điện mà hạt nhân của nguyên tử hydrogen tác dụng lên electron gây ra cho electron gia tốc hướng tâm, tức là
\[
k \frac{e^2}{r^2} = m_e \frac{v^2}{r} \quad \Rightarrow \quad v = \sqrt{\frac{k}{m_e r}} e = \sqrt{\frac{9 \cdot 10^9}{9{,}1 \times 10^{-31} \cdot 5{,}3 \times 10^{-11}}} \cdot 1{,}6 \times 10^{-19}
\]
\[
\approx 2{,}2 \times 10^6 \,\text{m/s}
\]
c) Sự chuyển động của electron quanh hạt nhân tạo nên một dòng điện tròn có cường độ
\[
I = \frac{e}{T} = \frac{e}{2\pi r / v} = \frac{ev}{2\pi r} = \frac{e^2}{2\pi r} \sqrt{\frac{k}{m_e r}}
\]
\[
= \frac{(1{,}6 \times 10^{-19})^2}{2\pi \cdot 5{,}3 \times 10^{-11}} \sqrt{\frac{9 \cdot 10^9}{9{,}1 \times 10^{-31} \cdot 5{,}3 \times 10^{-11}}} \approx 1{,}1 \times 10^{-3}\,A \approx 1\,\text{mA}
\]
d) Vì electron là hạt mang điện âm nên dòng điện tròn I do nó tạo ra có chiều ngược với chiều chuyển động của nó. Dùng quy tắc nắm bàn tay phải, ta suy ra chiều của vectơ cảm ứng từ $\vec{B}$ do dòng điện tròn $I$ gây ra tại hạt nhân nguyên tử hydrogen (chính là tại tâm của dòng điện tròn này) là chiều từ dưới lên (ngược lại với chiều ở hình vẽ của đề). Độ lớn cảm ứng từ này là
\[
B = 2\pi \cdot 10^{-7} \cdot \frac{I}{r} = 10^{-7} \cdot \frac{e^2}{r^2} \sqrt{\frac{k}{m_e r}}
\]
\[
= 10^{-7} \cdot \frac{(1{,}6 \times 10^{-19})^2}{(5{,}3 \times 10^{-11})^2} \cdot \sqrt{\frac{9 \cdot 10^9}{9{,}1 \times 10^{-31} \cdot 5{,}3 \times 10^{-11}}} \approx 12\,T
\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. từ trường mạnh.
B. điện trường mạnh.
C. tia Röntgen (tia X).
D. tia gamma (tia ) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.