Phỏng bạn Hùng và bạn Vương làm thí nghiệm trồng cây. Mỗi bạn trồng 40 cây cần tây trong cốc, phần
gốc của các cây khi bắt đầu trồng đều dài \(4{\rm{\;cm}}\). Bảng 1 và bảng 2 lần lượt biểu diễn mẫu số liệu ghép nhóm về số liệu thống kê chiều cao của các cây (đơn vị: centimét) mà bạn Hùng và bạn Vương trồng sau 5 tuần.
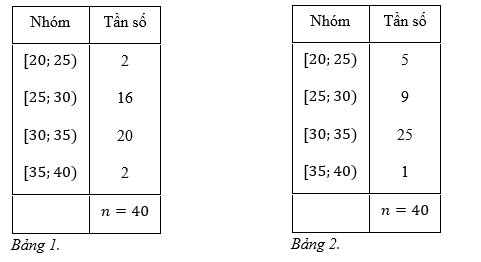
a) Chiều cao trung bình của mỗi cây do hai bạn Hùng và Vương trồng không bằng nhau.
b) Khoảng biến thiên của cả hai mẫu số liệu trên là 20.
c) Khoảng tứ phân vị của mẫu số liệu ở bảng 1 là 5,5.
d) Chiều cao của các cây mà bạn Vương trồng đồng đều hơn các cây mà bạn Hùng trồng.
Phỏng bạn Hùng và bạn Vương làm thí nghiệm trồng cây. Mỗi bạn trồng 40 cây cần tây trong cốc, phần
gốc của các cây khi bắt đầu trồng đều dài \(4{\rm{\;cm}}\). Bảng 1 và bảng 2 lần lượt biểu diễn mẫu số liệu ghép nhóm về số liệu thống kê chiều cao của các cây (đơn vị: centimét) mà bạn Hùng và bạn Vương trồng sau 5 tuần.
a) Chiều cao trung bình của mỗi cây do hai bạn Hùng và Vương trồng không bằng nhau.
b) Khoảng biến thiên của cả hai mẫu số liệu trên là 20.
c) Khoảng tứ phân vị của mẫu số liệu ở bảng 1 là 5,5.
d) Chiều cao của các cây mà bạn Vương trồng đồng đều hơn các cây mà bạn Hùng trồng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Chiều cao trung bình của cây do bạn Hùng trồng là: \(\overline {{x_H}} = 30,25\,\,\left( {{\rm{cm}}} \right)\).
Chiều cao trung bình của cây do bạn Vương trồng là: \(\overline {{x_V}} = 30,25\,\,\left( {{\rm{cm}}} \right)\).
Suy ra chiều cao trung bình của mỗi cây do hai bạn Hùng và Vương trồng là bằng nhau.
b) Khoảng biến thiên của cả hai mẫu số liệu là \(40 - 20 = 20\).
c) Xét mẫu số liệu ở bảng 1.
Tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó là:
\({Q_1} = 25 + \left( {\frac{{10 - 2}}{{16}}} \right) \cdot 5 = 27,5\,\,\left( {{\rm{cm}}} \right).\)
Tứ phân vi thứ ba \({Q_3}\) của mẫu số liệu đó là:
\({Q_3} = 30 + \left( {\frac{{30 - 18}}{{20}}} \right) \cdot 5 = 33\,\,\left( {{\rm{cm}}} \right).\)
Suy ra khoảng tứ phân vị của mẫu số liệu ở bảng 1 là \(33 - 27,5 = 5,5\).
c) Phương sai của mẫu số liệu ở bảng 1 là: \(s_H^2 = 11,1875\).
Phương sai của mẫu số liệu ở bảng 2 là: \(s_V^2 = 13,6875\).
Suy ra \(s_H^2 < s_V^2\). Vậy chiều cao của các cây mà bạn Hùng trồng đồng đều hơn các cây mà bạn Vương trồng.
Đáp án: a)S, b)Đ, c)Đ, d)S.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Cỡ mẫu \(n = 160\).
|
Lượng nước tiêu thụ \(\left( {{m^3}} \right)\) |
\([3;6)\) |
\([6;9)\) |
\([9;12)\) |
\([12;15)\) |
\([15;18)\) |
|
Giá trị đại diện |
4,5 |
7,5 |
10,5 |
13,5 |
16,5 |
|
Số hộ gia đình |
24 |
57 |
42 |
29 |
8 |
\[\bar x = \frac{1}{{160}}(24 \cdot 4,5 + 57 \cdot 7,5 + 42 \cdot 10,5 + 29 \cdot 13,5 + 8 \cdot 16,5) \approx 9,4\,\,\left( {{m^3}} \right).\]
Vậy lượng nước tiêu thụ trung bình trong tháng của một hộ gia đình trong khu vực nói trên xấp xỉ bằng \[9,4\,\,\left( {{m^3}} \right).\]
b) Khoảng biến thiên của mẫu số liệu trên là \(R = 18 - 3 = 15\,\,\left( {{m^3}} \right).\)
c) \(25\% \) các hộ gia đình có lượng nước tiêu thụ cao nhất có lượng nước tiêu thụ không nhỏ hơn \({Q_3}\), với \({Q_3}\) là tứ phân vị thứ ba của mẫu số liệu.
Nhóm \([9;12)\) là nhóm đầu tiên có tần số tích luỹ \( \ge \frac{{3.160}}{4} = 120,\)suy ra tứ phân vị thứ ba của mẫu số liệu là \({Q_3} = 9 + \frac{{\frac{{160.3}}{4} - (24 + 57)}}{{42}} \cdot (12 - 9) \approx 11,79\,\,\left( {{m^3}} \right).\)
Vậy công ty nên gửi thông báo tiết kiệm nước đến các hộ gia đình có lượng nước tiêu thụ từ \(11,79\;{m^3}\) nước trở lên.
d) Ta có \[{s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + {n_3}{{\left( {{x_3} - \overline x } \right)}^2} + {n_4}{{\left( {{x_4} - \overline x } \right)}^2} + {n_5}{{\left( {{x_5} - \overline x } \right)}^2}}}{n} \approx 10,77.\]
Suy ra độ lệch chuẩn của mẫu số liệu trên xấp xỉ bằng \(3,28\,\,\left( {{m^3}} \right).\)
Đáp án: a)Đ, b)Đ, c)S, d)S.
Lời giải
Trong mẫu số liệu ghép nhóm đó, ta có: đầu mút trái của nhóm 1 là \({a_1} = 8\), đầu mút phải của nhóm 5 là \({a_6} = 23\).
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = {a_6} - {a_1} = 23 - 8 = 15\).chọn D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo