Cho hình hộp \[ABCD.A'B'C'D'\]. Xét các điểm \[M,N\] lần lượt thuộc các đường thẳng \[A'C\,,\,C'D\]sao cho đường thẳng \[MN\] song song với đường thẳng \[BD'\]. Khi đó tỉ số \(\frac{{MN}}{{BD'}}\) bằng ……….
Câu hỏi trong đề: Đề kiểm tra Vectơ trong không gian (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
![Cho hình hộp \[ABCD.A'B'C'D'\]. Xét các điểm \[M,N\] lần lượt thuộc các đường thẳng \[A'C\,,\,C'D\]sao cho đường thẳng \[MN\] song song với đường thẳng \[BD'\]. Khi đó tỉ số \(\frac{{MN}}{{BD'}}\) bằng ………. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/30-1759239791.png)
Đặt \(\overrightarrow {BA} = \vec x\), \(\overrightarrow {BB'} = \vec y\), \(\overrightarrow {BC} = \vec z\).
Do \(\overrightarrow {CM} \), \(\overrightarrow {CA'} \) là hai vectơ cùng phương \( \Rightarrow \exists \,k \in \mathbb{R}:\,\overrightarrow {CM} = k.\overrightarrow {CA'} \).
Và \(\overrightarrow {C'N} \), \(\overrightarrow {C'D} \) là hai vectơ cùng phương \( \Rightarrow \exists \,h \in \mathbb{R}:\,\overrightarrow {C'N} = h.\overrightarrow {C'D} \).
Ta có: \[\overrightarrow {BD'} = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow x + \overrightarrow y + \overrightarrow z \], (1)
Ta lại có: \(\overrightarrow {MN} = \overrightarrow {CN} - \overrightarrow {CM} = \overrightarrow {CC'} + \overrightarrow {C'N} - \overrightarrow {CM} = \overrightarrow {CC'} + h.\overrightarrow {C'D} - k.\overrightarrow {CA'} \)
\( = \overrightarrow y + h.( - \overrightarrow y + \overrightarrow x ) - k.\left( {\overrightarrow y - \overrightarrow z + \overrightarrow x } \right) = \left( {h - k} \right).\overrightarrow x + \left( {1 - h - k} \right).\overrightarrow y + k.\overrightarrow z \), (2)
Do \(MN\parallel B'D\) nên tồn tại . Từ (1) và (2) ta có\(\left\{ \begin{array}{l}h - k = t\\1 - h - k = t\\k = t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = t\\h = 2t\\1 - 3t = t\end{array} \right. \Rightarrow t = \frac{1}{4} \Rightarrow \overrightarrow {MN} = \frac{1}{4}\overrightarrow {BD'} \).
Vậy \(\frac{{MN}}{{BD'}} = \frac{1}{4}\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\overrightarrow {GA} + \overrightarrow {GC} = 2\overrightarrow {GM} \).
B. \(\overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow {MN} \).
C. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
D. \(2\overrightarrow {NM} = \overrightarrow {AB} + \overrightarrow {CD} \).
Lời giải
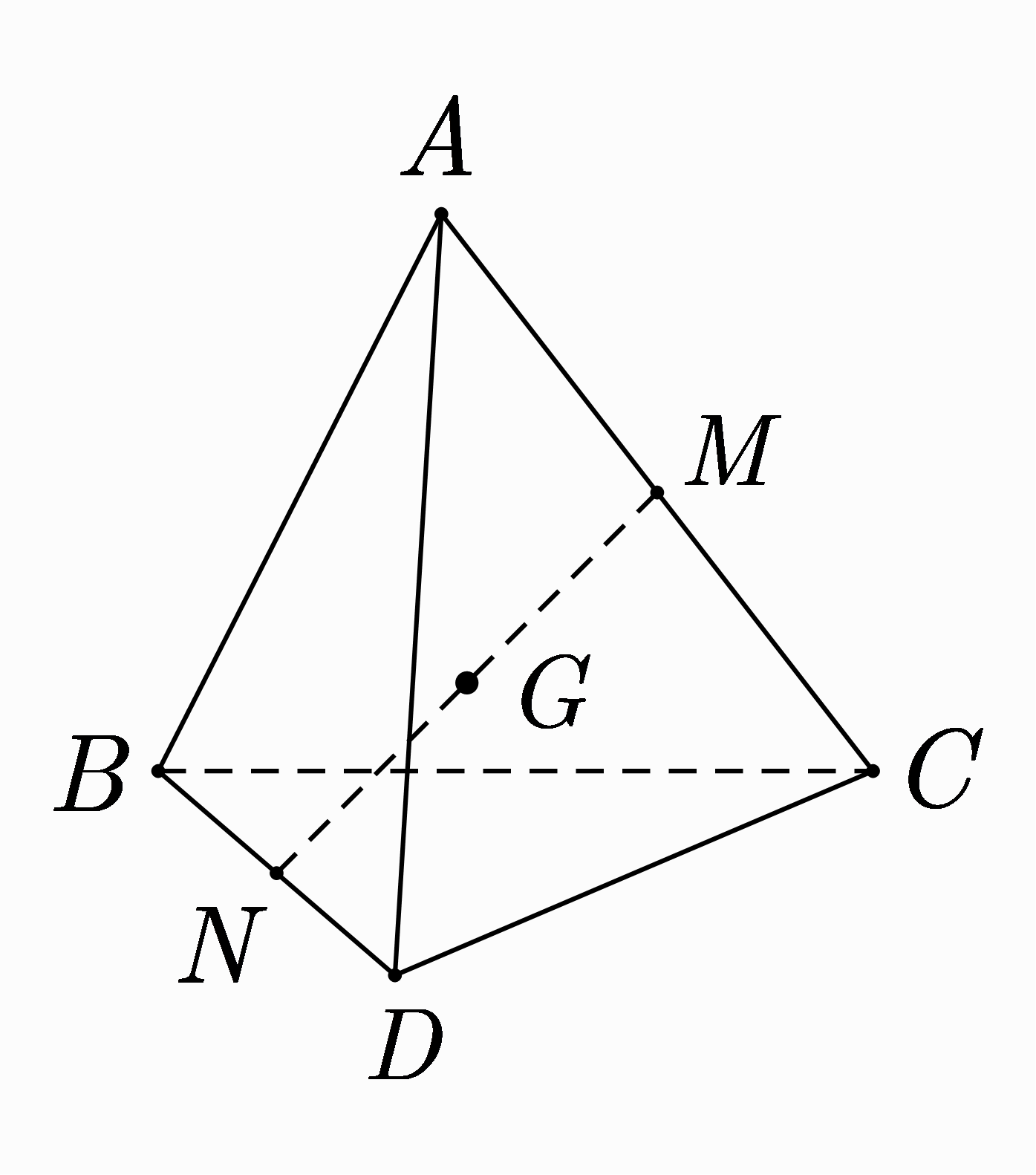
Ta có: \(\overrightarrow {GA} + \overrightarrow {GC} = 2\overrightarrow {GM} \) nên đáp án A đúng.
\(\overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow {MN} \) đúng vì \(\overrightarrow {GB} + \overrightarrow {GD} = 2\overrightarrow {GN} = \overrightarrow {MN} \)
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\) đúng vì \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 2\left( {\overrightarrow {GM} + \overrightarrow {GN} } \right) = \overrightarrow 0 \).
Đáp án D: \(2\overrightarrow {NM} = \overrightarrow {AB} + \overrightarrow {CD} \) sai vì :
\[\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} = \left( {\overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NB} } \right) + \left( {\overrightarrow {CM} + \overrightarrow {MN} + \overrightarrow {ND} } \right)\\ = 2\overrightarrow {MN} + \left( {\overrightarrow {AM} + \overrightarrow {CM} } \right) + \left( {\overrightarrow {NB} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} + \overrightarrow 0 + \overrightarrow 0 = 2\overrightarrow {MN} .\end{array}\]
Lời giải
1. Mệnh đề sai vì \(G\) là trọng tâm của tam giác \(BCD\) nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
2. Mệnh đề đúng: Vì
\(\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow {IG} + \overrightarrow {GB} + \overrightarrow {IG} + \overrightarrow {GC} + \overrightarrow {IG} + \overrightarrow {GD} = 3\overrightarrow {IG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 3\overrightarrow {IG} \).
3. Mệnh đề đúng: Vì \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)\(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow {IA} + 3\overrightarrow {IG} = \overrightarrow {IA} + \overrightarrow {AI} = \overrightarrow 0 \).
4. .Mệnh đề đúng vì:
\(\overrightarrow {AI} = 3\overrightarrow {IG} \Leftrightarrow \overrightarrow {IA} = - \frac{3}{4}\overrightarrow {AG} \).
\[\overrightarrow {IB} = \overrightarrow {IA} + \overrightarrow {AB} = - \frac{3}{4}\overrightarrow {AG} + \overrightarrow {AB} = - \frac{3}{4}.\frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right) + \overrightarrow {AB} = \frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} - \frac{1}{4}\overrightarrow {AD} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\(\overrightarrow {AC} = \overrightarrow {C'A'} \)
B.\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC} = \overrightarrow {AA'} \).
C. \(\overrightarrow {AB} = \overrightarrow {CD} \).
D.\(\overrightarrow {AB} + \overrightarrow {C'D'} = \overrightarrow 0 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo