Trong không gian \[Oxyz\] tìm tọa độ của điểm \[A\] biết điểm \[A\] nằm trên tia \[Oy\] và \[OA = 3\].
Trong không gian \[Oxyz\] tìm tọa độ của điểm \[A\] biết điểm \[A\] nằm trên tia \[Oy\] và \[OA = 3\].
Câu hỏi trong đề: Đề kiểm tra Hệ trục tọa độ trong không gian (có lời giải) !!
Quảng cáo
Trả lời:
Ta có: \[A\] nằm trên tia \[Oy\] và \[OA = 3\] nên \[\overrightarrow {OA} = 3\overrightarrow j \] suy ra \[A\left( {0;\,3;\,0} \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
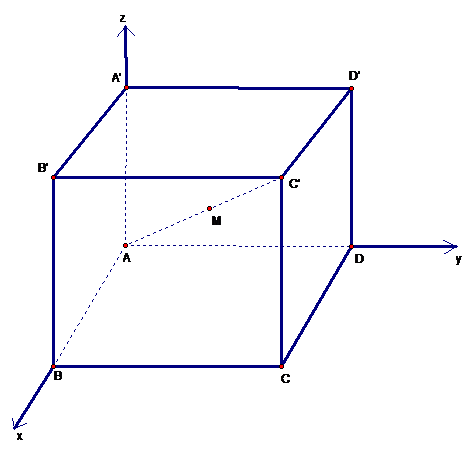
Từ giả thiết ta có \(A\left( {0;0;0} \right),C\left( {4;8;10} \right)\)
Gọi \(M\)là tâm của hình hộp. Khi đó \(M\)là trung diểm của \(AC'\)
Suy ra \(M\left( {2;4;5} \right)\)
Lời giải
Đáp số: \(C'\left( {2;2;2} \right)\).
Ta có:\(A\left( {0;0;0} \right),B\left( {2;0;0} \right);D\left( {0;2;0} \right);A'\left( {0;0;2} \right)\)
\( \Rightarrow C\left( {2;2;0} \right);B'\left( {2;0;2} \right);D'\left( {0;2;2} \right);C'\left( {2;2;2} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vec tơ \(\overrightarrow a \left( {1;\,\, - 2;\,\,0} \right)\) và \(\overrightarrow b \left( { - 2;\,\,3;\,\,1} \right)\). Xét tính đúng sai của các mệnh đề sau:
a) \(\overrightarrow a .\overrightarrow b = - 8\).
b) \(\left| {\overrightarrow b } \right| = 14\).
c) \(\overrightarrow a + \overrightarrow b = \left( { - 1;\,\,1;\,\, - 1} \right)\).
d) \(2\overrightarrow a = \left( {2;\,\, - 4;\,\,2} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vec tơ \(\overrightarrow a \left( {1;\,\, - 2;\,\,0} \right)\) và \(\overrightarrow b \left( { - 2;\,\,3;\,\,1} \right)\). Xét tính đúng sai của các mệnh đề sau:a) \(\overrightarrow a .\overrightarrow b = - 8\).
b) \(\left| {\overrightarrow b } \right| = 14\).
c) \(\overrightarrow a + \overrightarrow b = \left( { - 1;\,\,1;\,\, - 1} \right)\).
d) \(2\overrightarrow a = \left( {2;\,\, - 4;\,\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.