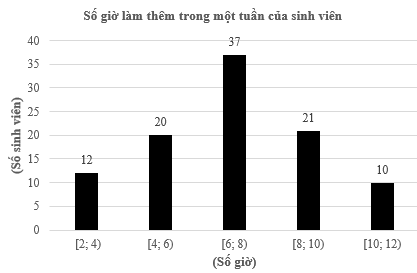
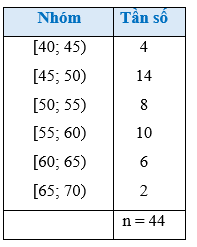
Tổng hợp tiền lương tháng của một số nhân viên văn phòng được ghi lại như sau (đơn vị: triệu đồng):
|
Lương tháng (triệu đồng) |
\([6;8)\) |
\([8;10)\) |
\([10;12)\) |
\([12;14)\) |
|
Số nhân viên |
3 |
6 |
8 |
7 |
Giá trị nào sau đây là giá trị ngoại lệ của mẫu số liệu trên
A. \(3\).
B. \(9\).
C. \(15\).
D. \(10\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
c) Gọi \({x_1};{x_2}; \ldots ;{x_{24}}\) lần lượt là lương tháng của mỗi nhân viên được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_6} + {x_7}} \right)\).
Do \({x_6},{x_7} \in [8;10)\) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 8 + \frac{{\frac{{24}}{4} - 3}}{6}(10 - 8) = 9\)
Tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right)\).
Do \({x_{18}},{x_{19}} \in [12;14)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 12 + \frac{{\frac{{3.24}}{4} - 17}}{7}(14 - 12) = 12,3.\)
Vậy khoảng tứ phân vị là: \(\Delta Q = {Q_3} - {Q_1} = 12,3 - 9 = 3,3\).
\(\left[ {{Q_1} - 1,5\Delta Q;{Q_3} + 1,5\Delta Q} \right] = \left[ {4,05;17,25} \right]\). Vậy giá trị ngoại lệ là 38.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:
|
Thời gian luyện tập (giờ) |
\([0;2)\) |
\([2;4)\) |
\([4;6)\) |
\([6;8)\) |
\([8;10)\) |
|
Số vận động viên |
3 |
8 |
12 |
12 |
4 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
A. 3,6875.
B. 5,417.
C. \(5,3545\).
D. 7,68.
Lời giải
Chọn C
Tứ phân vị thứ ba của dãy số liệu \({x_1};{x_2}; \ldots ;{x_{39}}\) là \({x_{30}} \in [6;8)\).
Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là
\({Q_3} = 6 + \frac{{\frac{{3.39}}{4} - (3 + 8 + 12)}}{{12}} \cdot (8 - 6) = \frac{{169}}{{24}} \approx 7,042\).
Tứ phân vị thứ nhất của dãy số liệu \({x_1};{x_2}; \ldots ;{x_{39}}\) là \({x_{10}} \in [2;4)\).
Do đó, tứ phân vị thứ nhất của mẫu số liệu là
\(n = 39,{n_m} = 8,C = 11,{u_m} = 2,{u_{m + 1}} = 4\)
\({Q_1} = 2 + \frac{{\frac{{1.39}}{4} - 11}}{8}(4 - 2) \approx 1,6875\).
Vậy khoảng tứ phân vị \(\Delta Q = {Q_3} - {Q_1} = 7,042 - 1,6875 = 5,3545\).
Câu 2
A. \(25\).
B. \(20\).
C. \(15\).
D. \(10\).
Lời giải
Chọn D
Ta có: \({Q_1} = 50 + \frac{{8 - 4}}{6}.10 = \frac{{170}}{3}\); \({Q_3} = 70 + \frac{{24 - 20}}{6}.10 = \frac{{230}}{3}\).
Vậy khoảng tứ phân vị của mẫu số liệu trên là: \(\Delta Q = {Q_3} - {Q_1} = 20\).
Câu 3
Ta có bảng sau về thời gian tập thể dục buổi sáng của bác Bình và bác An:
|
Thời gian (phút) |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
[35; 40) |
|
Bác Bình |
5 |
12 |
8 |
3 |
2 |
|
Bác An |
0 |
25 |
5 |
0 |
0 |
Hỏi hiệu khoảng biến thiên của mẫu số liệu của bác An và bác Bình là bao nhiêu?
A. \(11\).
B. \(9\).
C. \(15\).
D. \(10\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(15,5\).
B. \(13,5\).
C. \(15,3\).
D. \(13,3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(11\).
B. \(9\).
C. \(15\).
D. \(10\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
|
Điện lượng (nghìn mAh) |
\([0,9;0,95)\) |
\([0,95;1,0)\) |
\([1,0;1,05)\) |
\([1,05;1,1)\) |
\([1,1;1,15)\) |
|
Số viên pin |
10 |
20 |
35 |
15 |
5 |
Tìm khoảng tứ phân vị của dãy số liệu trên.
A. \(0.68\).
B. \(0.068\).
C. \(0,608\).
D. \(0,806\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo