Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ \(Oxyz\) được thiết lập như hình bên dưới, cho biết \(M\) là vị trí của máy bay, \(OM = 14,\,\,\widehat {NOB} = 32^\circ ,\,\,\widehat {MOC} = 65^\circ \). Tìm tọa độ điểm \(M\).
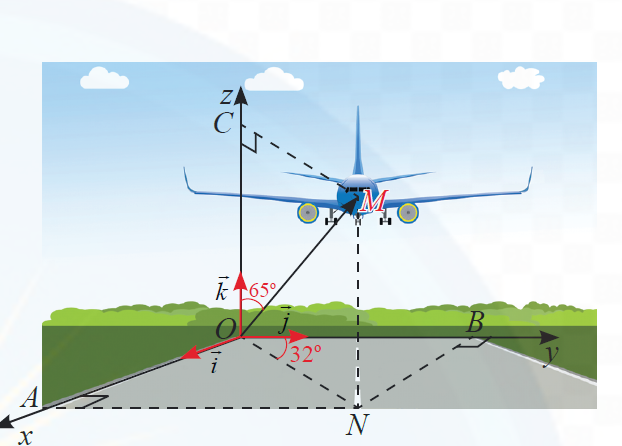
Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ \(Oxyz\) được thiết lập như hình bên dưới, cho biết \(M\) là vị trí của máy bay, \(OM = 14,\,\,\widehat {NOB} = 32^\circ ,\,\,\widehat {MOC} = 65^\circ \). Tìm tọa độ điểm \(M\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tam giác \(OCM\) vuông tại \(C\) có
\(OC = OM.\cos 65^\circ = 14.\cos 65^\circ \approx 5,9\) và \(CM = OM.\sin 65^\circ = 14.\sin 65^\circ \approx 12,7\).
\(ON = CM,\,\,AN = OB\).
Có \(\widehat {AON} = 90^\circ - \widehat {BON} = 58^\circ \)
Tam giác \(OAN\) vuông tại \(A\) có
\(OA = ON.\cos 58^\circ = 12,7.\cos 58^\circ \approx 6,7\) và \(AN = ON.\sin 58^\circ = 12,7.\sin 58^\circ \approx 10,8\).
\(\overrightarrow {OM} = OA.\overrightarrow i + OB.\overrightarrow j + OC.\overrightarrow k = 6,7.\overrightarrow i + 10,8.\overrightarrow j + 5,9.\overrightarrow k \).
Vậy \(M\left( {6,7;10,8;5,9} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Đúng |
b) Sai |
c) Sai |
d) Đúng |
a) Ta có \(A\left( {1; - 2;3} \right),\,\,B\left( { - 2;1;2} \right) \Rightarrow \overrightarrow {AB} = \left( { - 3;3; - 1} \right)\). Suy ra a) đúng.
b) Ta có \(A\left( {1; - 2;3} \right),\,\,C\left( {3; - 1;2} \right) \Rightarrow \overrightarrow {AC} = \left( {2;1; - 1} \right)\). Suy ra b) sai.
c) Do \(3\overrightarrow {AC} = \left( {6;3; - 3} \right);\,\overrightarrow {AB} = \left( { - 3;3; - 1} \right)\). Suy ra c) sai.
d) Ta có\(\overrightarrow {AB} = \left( { - 3;3; - 1} \right);\,\overrightarrow {AC} = \left( {2;1; - 1} \right) \Rightarrow \frac{{ - 3}}{2} \ne \frac{3}{1} \Rightarrow \overrightarrow {AB} \), \(\overrightarrow {AC} \) không cùng phương. Suy ra ba điểm \(A,\,B,\,C\) không thẳng hàng. Suy ra d) đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Đúng |
b) Đúng |
c) Đúng |
d) Sai |
a) Ta có \(A\left( {2; - 1; - 2} \right),\,\,B\left( {3;1;2} \right) \Rightarrow \overrightarrow {AB} = \left( {1;2;4} \right)\). Suy ra a) đúng.
b) Ta có \(C\left( {1; - 1;1} \right);D\left( {{x_D};{y_D};{z_D}} \right) \Rightarrow \overrightarrow {DC} = \left( {1 - {x_D}; - 1 - {y_D};1 - {z_D}} \right)\). Suy ra b) đúng.
c) Do hình bình hành \(ABCD\) có \(\overrightarrow {AB} = \overrightarrow {DC} \). Suy ra c) đúng.
d) Do hình bình hành \(ABCD\) có \(\overrightarrow {AB} = \overrightarrow {DC} \).
Mà \(\overrightarrow {AB} = \left( {1;2;4} \right);\,\,\overrightarrow {DC} = \left( {1 - {x_D}; - 1 - {y_D};1 - {z_D}} \right) \Rightarrow \left\{ \begin{array}{l}1 = 1 - {x_D}\\2 = - 1 - {y_D}\\4 = 1 - {z_D}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = - 3\\{z_D} = - 3\end{array} \right.\).
Vậy \(D\left( {0; - 3; - 3} \right)\). Suy ra d) sai.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập