Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là \(10\)m, chiều rộng là \(8\)m và chiều cao là \(4\)m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục toạ độ \(Oxyz\) có gốc \(O\) trùng với một góc phòng và mặt phẳng \((Oxy)\) trùng với mặt sàn, đơn vị đo được lấy theo mét (Hình vẽ).
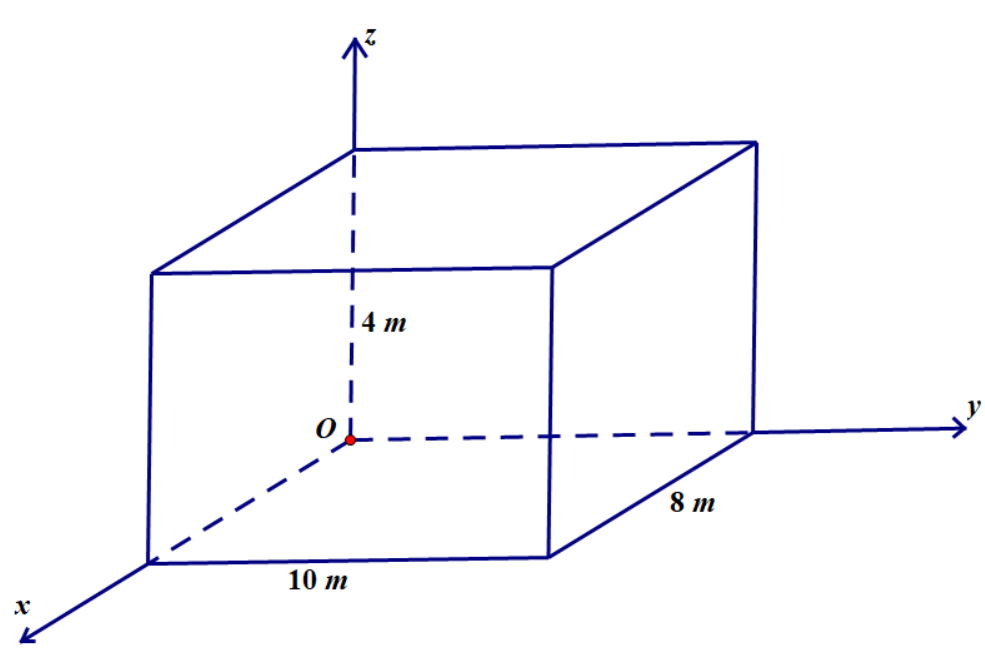
Tính khoảng cách từ điểm treo bóng đèn đến góc phòng học (kết quả làm tròn đến hàng phần trăm).
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là \(10\)m, chiều rộng là \(8\)m và chiều cao là \(4\)m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục toạ độ \(Oxyz\) có gốc \(O\) trùng với một góc phòng và mặt phẳng \((Oxy)\) trùng với mặt sàn, đơn vị đo được lấy theo mét (Hình vẽ).

Tính khoảng cách từ điểm treo bóng đèn đến góc phòng học (kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Với hệ trục toạ độ \(Oxyz\) có gốc \(O\) trùng với một góc phòng và mặt phẳng \((Oxy)\) trùng với mặt sàn, đơn vị đo được lấy theo mét.
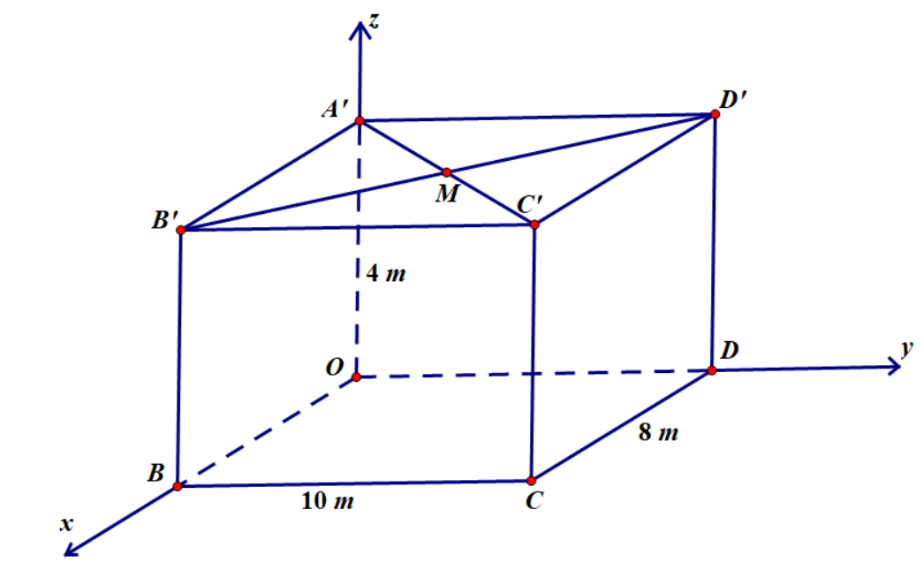
Phòng học thiết kế dạng hình hộp chữ nhật \(OBCD.A'B'C'D'\) với \(A'B'C'D'\) là hình chữ nhật. Gọi \(M\) là giao điểm của hai đường chéo \[A'C'\] và \[B'D'\] nên \(M\) là trung điểm của \[A'C'\] với \[A'\left( {0;0;4} \right)\], \[C'\left( {8;10;4} \right)\].
Vì đèn được treo tại chính giữa trần nhà của phòng học nên điểm treo bóng đèn trùng với điểm \(M\).
Có \(\left\{ \begin{array}{l}{x_M} = \frac{{{x_{A'}} + {x_{C'}}}}{2} = 4\\{y_M} = \frac{{{y_{A'}} + {y_{C'}}}}{2} = 5\\{z_M} = \frac{{{z_{A'}} + {z_{C'}}}}{2} = 4\end{array} \right.\) nên \(M(4;5;4)\), khoảng cách từ điểm treo bóng đèn đến góc phòng học là \(OM = \sqrt {{4^2} + {5^2} + {4^2}} = \sqrt {57} \approx 7,55\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) |
b) |
c) |
d) |
|
Đúng |
Sai |
Sai |
Đúng |
a) \(\overrightarrow {OM} = \left( {50;120;4} \right) \Rightarrow OM = \sqrt {{{50}^2} + {{120}^2} + {4^2}} \approx 130,06\)
Vậy khoảng cách giữa máy bay và trạm không lưu tại thời điểm 8h xấp xỉ 130km.
b) Ta có \(\overrightarrow {OM} + \vec v = \left( {350;520;7} \right)\)
Tại thời điểm 9h, tọa độ của máy bay là \({M_1}\left( {350;520;7} \right)\)
Vậy độ cao của máy bay so với mặt đất là 7km.
c) Ta có \(\overrightarrow {OM} + 2\vec v = \left( {650;920;10} \right)\).
Vậy tại thời điểm 10h, tọa độ của máy bay là \({M_2}\left( {650;920;10} \right)\)
Ta có: \(\overrightarrow {{M_2}F} = \left( {600;100;10} \right) \Rightarrow {M_2}F = \sqrt {{{600}^2} + {{100}^2} + {{10}^2}} \approx 608,36\)
Vậy khoảng cách giữa máy bay và tháp truyền hình \(F\) xấp xỉ 600km.
d) Từ độ cao 10km, với tốc độ hạ độ cao là 5km/h thì máy bay cần 2h để đáp xuống đất.
Ta có: \(\overrightarrow {O{M_2}} + 2\overrightarrow {{v_2}} = \left( {1450;1520;0} \right)\).
Vậy tọa độ của máy bay khi đáp xuống là \({M_3}\left( {1450;1520;0} \right)\)
Lời giải
![Trong không gian với hệ tọa độ \(Oxyz\), cho hình vuông \(ABCD\) với \[B\left( {3;0;8} \right)\], \[D\left( { - 5; - 4;0} \right)\], \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = a\sqrt b \). Tính giá trị biểu thức \(M = a + 2b\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/16-1759368180.png)
Dựng hình bình hành \(ACBE\). Ta có: \(\overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow {CE} \).
Trong không gian với hệ tọa độ \(Oxyz\), ta có \(BD = \sqrt {{{( - 5 - 3)}^2} + {{( - 4 - 0)}^2} + {{(0 - 8)}^2}} = 12\).
Có \(ABCD\) là hình vuông nên \(AC = BD = 12\). Suy ra \(CD = 6\sqrt 2 \) , \(DE = 12\sqrt 2 \). Tam giác \(CDE\) vuông tại \(D\).
Có \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = CE = \sqrt {C{D^2} + D{E^2}} = \sqrt {{{\left( {6\sqrt 2 } \right)}^2} + {{\left( {12\sqrt 2 } \right)}^2}} = 6\sqrt {10} \).
Suy ra \(a = 6;\,\,\,b = 10\); \(M = a + 2b = 26\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Ta có: \[\left| {\overrightarrow P } \right| = P = m.g = 20.9,8 = 196(N)\]. \[\left| {\overrightarrow d } \right| = \left| {\overrightarrow {AC} } \right| = AC = 3(m)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/19-1759368263.png)