PHẦN 2. CÂU HỎI DẠNG ĐÚNG – SAI (4 CÂU)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Trên các cạnh \[CD\] và \[BB'\] ta lần lượt lấy các điểm M và N sao cho \[DM = BN = x\] với \[0 \le x \le a\]. Các mệnh đề dưới đây đúng hay sai?
a) \(\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {A{\rm{D}}} \)
b) Gọi \[K\] là trung điểm \(AD\) khi đó \(\overrightarrow {C'K} = \overrightarrow {C'C} + \overrightarrow {C'D'} + \frac{1}{2}\overrightarrow {C'B'} \).
c) \(\overrightarrow {AB} .\overrightarrow {B'D'} = {a^2}\).
d) Góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng \(60^\circ \).
PHẦN 2. CÂU HỎI DẠNG ĐÚNG – SAI (4 CÂU)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Trên các cạnh \[CD\] và \[BB'\] ta lần lượt lấy các điểm M và N sao cho \[DM = BN = x\] với \[0 \le x \le a\]. Các mệnh đề dưới đây đúng hay sai?a) \(\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {A{\rm{D}}} \)
b) Gọi \[K\] là trung điểm \(AD\) khi đó \(\overrightarrow {C'K} = \overrightarrow {C'C} + \overrightarrow {C'D'} + \frac{1}{2}\overrightarrow {C'B'} \).
c) \(\overrightarrow {AB} .\overrightarrow {B'D'} = {a^2}\).
d) Góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng \(60^\circ \).
Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
a) Đúng.
b) Đúng.
Ta có: \(\overrightarrow {C'K} = \overrightarrow {C'C} + \overrightarrow {CK} = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CD} } \right) = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {C'A'} + \overrightarrow {C'D'} } \right)\)
\( = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {C'D'} } \right) = \overrightarrow {C'C} + \frac{1}{2}\overrightarrow {C'B'} + \overrightarrow {C'D'} \)
c) Sai.
Ta có: \[\overrightarrow {AB} .\overrightarrow {B'D'} = \left( {\overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {B'B} } \right).\overrightarrow {B'D'} = \overrightarrow {AA'} .\overrightarrow {B'D'} + \overrightarrow {A'B'} .\overrightarrow {B'D'} + \overrightarrow {B'B} .\overrightarrow {B'D'} = \overrightarrow {A'B'} .\overrightarrow {B'D'} \]
\( = A'B'.B'D'.{\rm{cos}}\left( {\overrightarrow {A'B'} ,\overrightarrow {B'D'} } \right) = a.a\sqrt 2 .{\rm{cos}}\left( {135^\circ } \right) = - {a^2}\)
d) Đúng.
Ta đặt \[\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \]. Ta có \[\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = \left| {\overrightarrow c } \right| = a\]
\[\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} \] hay \[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b + \overrightarrow c \]
Mặt khác
\[\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \left( {\overrightarrow {AB} + \overrightarrow {BN} } \right) - \left( {\overrightarrow {AD} + \overrightarrow {DM} } \right)\] với \[\overrightarrow {BN} = \frac{x}{a}.\overrightarrow a \] và \[\overrightarrow {DM} = \frac{x}{a}.\overrightarrow b \]
Do đó \[\overrightarrow {MN} = \left( {\overrightarrow b + \frac{x}{a}\overrightarrow a } \right) - \left( {\overrightarrow c + \frac{x}{a}\overrightarrow b } \right) = \frac{x}{a}\overrightarrow a + \left( {a - \frac{x}{a}} \right)\overrightarrow b - \overrightarrow c \]
Ta có \[\overrightarrow {AC'} .\overrightarrow {MN} = \left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\left[ {\frac{x}{a}\overrightarrow a + \left( {a - \frac{x}{a}} \right)\overrightarrow b - \overrightarrow c } \right]\]
Vì \[\overrightarrow a .\overrightarrow b = 0,\overrightarrow a .\overrightarrow c = 0,\overrightarrow b .\overrightarrow c = 0\] nên ta có
\[\overrightarrow {AC'} .\overrightarrow {MN} = \frac{x}{a}{\overrightarrow a ^2} + \left( {1 - \frac{x}{a}} \right){\overrightarrow b ^2} - {\overrightarrow c ^2} = x.a + \left( {1 - \frac{x}{a}} \right){a^2} - {a^2} = 0\], vậy góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng \(90^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
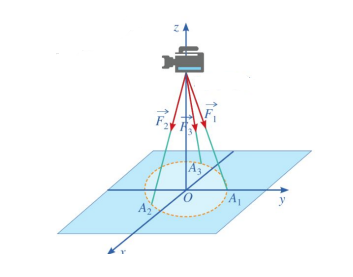
Ta có: \(\overrightarrow {E{A_1}} = \left( {0;1; - 8} \right)\),\(\overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\), \(\overrightarrow {E{A_3}} = \left( {\frac{{ - \sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\) Nên \(E{A_1} = E{A_2} = E{A_3} = \sqrt {65} \)
Mặt khác, \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) vì đèn cân bằng và trọng lực của đèn tác dụng đều lên 3 chân của giá đỡ
Do đó : \(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} = \left( {0;k; - 8k} \right)\),\[\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\],\(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} = \left( {\frac{{ - \sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\)
\( \Rightarrow {\overrightarrow F _1} + \overrightarrow {{F_2}} + {\overrightarrow F _3} = \left( {0;0; - 24k} \right)\)
Mà \({\overrightarrow F _1} + \overrightarrow {{F_2}} + {\overrightarrow F _3} = \overrightarrow P = \left( {0;0; - 240} \right) \Rightarrow - 24k = - 240 \Rightarrow k = 10\)
Vậy \(\overrightarrow {{F_1}} = \left( {0;10; - 80} \right)\)
Lời giải
a) Đúng.
Ta có\[\overrightarrow {AB} = \left( {2; - 2;0} \right)\], \[\overrightarrow {BC} = \left( { - 1;1; - 1} \right)\]. Suy ra \[\overrightarrow {AB} \ne k\overrightarrow {BC} \]với mọi \[k \in \mathbb{R}\] nên ba điểm \[A\], \[B\], \[C\] không thẳng hàng.
b) Đúng.
Ta có\[\overrightarrow {AC} = \left( {1; - 1; - 1} \right)\], \[\overrightarrow {AM} = \left( {a - 1;b - 1;1} \right)\].
Ba điểm \[A\], \[C\], \[M\] thẳng hàng suy ra \[\overrightarrow {AB} = k.\overrightarrow {AM} \Leftrightarrow \left\{ \begin{array}{l}1 = k.\left( {a - 1} \right)\\ - 1 = k.\left( {b - 1} \right)\\ - 1 = k.1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 2\\k = - 1\end{array} \right.\].
Vậy \[a + b = 0 + 2 = 2\]
c) Sai.
\[\cos \alpha = \cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {BC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{2.\left( { - 1} \right) + \left( { - 2} \right).1 + 0.\left( { - 1} \right)}}{{2\sqrt 2 .\sqrt 3 }} = - \frac{{\sqrt 6 }}{3}\].
d) Sai.
\[\overrightarrow {AB} = \left( {2; - 2;0} \right)\], \[\overrightarrow {AM} = \left( { - 1;1;1} \right)\].
\[\left[ {\overrightarrow {AB} ,\overrightarrow {AM} } \right] = \left( { - 2; - 2;4} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.