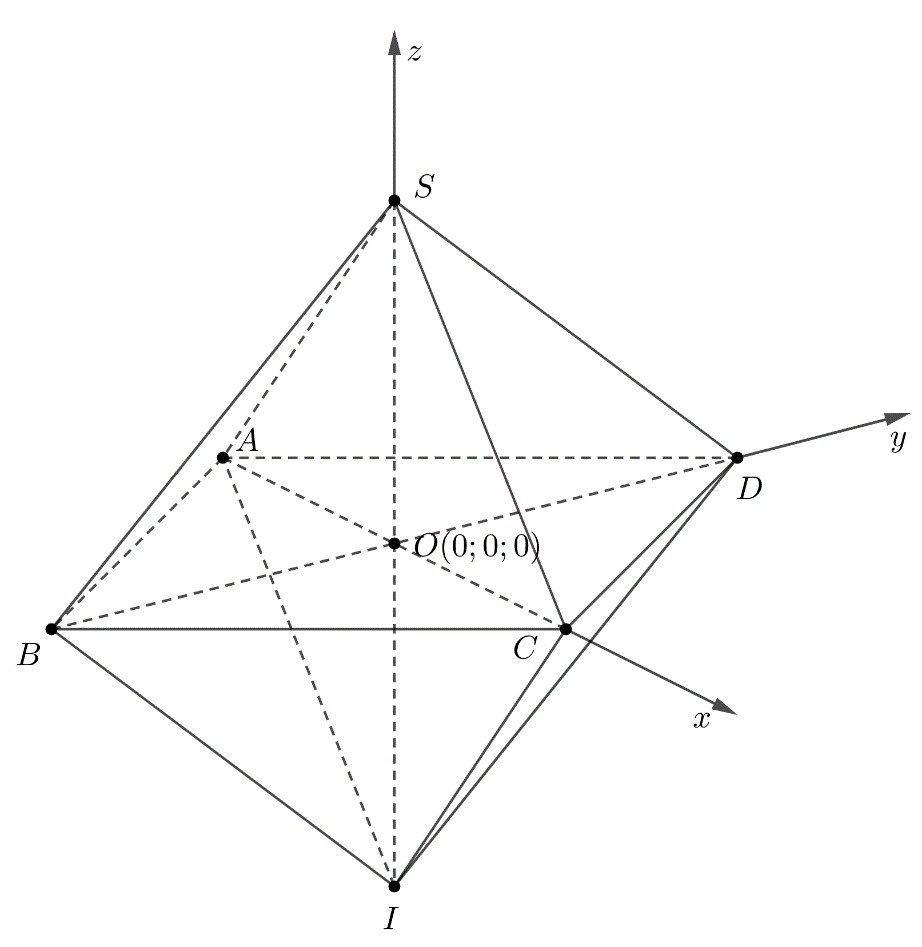
Một chi tiết trong bộ trang sức có hình bát diện đều, được gắn hệ trục tọa độ Oxyz như hình vẽ. Các hình chóp S.ABCD và I.ABCD là các hình chóp tứ giác đều cạnh \(1\,{\rm{cm}}\).
a) Tính tổng hoành độ các đỉnh \(S,A,B,C,D,I\).
b) Tính số đo góc nhị diện \[\left[ {S;CD;I} \right]\] theo đơn vị độ, làm tròn đến hàng đơn vị.
Một chi tiết trong bộ trang sức có hình bát diện đều, được gắn hệ trục tọa độ Oxyz như hình vẽ. Các hình chóp S.ABCD và I.ABCD là các hình chóp tứ giác đều cạnh \(1\,{\rm{cm}}\).

a) Tính tổng hoành độ các đỉnh \(S,A,B,C,D,I\).
b) Tính số đo góc nhị diện \[\left[ {S;CD;I} \right]\] theo đơn vị độ, làm tròn đến hàng đơn vị.
Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
a) Đáp số: \(0\).
Ta có \(OA = OB = OC = OD = \frac{{\sqrt 2 }}{2}\) nên \(A\left( { - \frac{1}{{\sqrt 2 }};0;0} \right),B\left( {0; - \frac{1}{{\sqrt 2 }};0} \right)\)\(,C\left( {\frac{1}{{\sqrt 2 }};0;0} \right)\),
\(D\left( {0;\frac{1}{{\sqrt 2 }};0} \right)\)
Ta có \(OI = SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}} = \frac{1}{{\sqrt 2 }}\) nên \(S\left( {0;0;\frac{1}{{\sqrt 2 }}} \right),I\left( {0;0; - \frac{1}{{\sqrt 2 }}} \right)\).
Tổng hoành độ các đỉnh \(S,A,B,C,D,I\) là:
\( - \frac{1}{{\sqrt 2 }} + 0 + \frac{1}{{\sqrt 2 }} + 0 + 0 + 0 = 0\).
b) Đáp số: \(109\).
Gọi \(M\) là trung điểm của \(CD\) thì \(M\left( {\frac{1}{{2\sqrt 2 }};\frac{1}{{2\sqrt 2 }};0} \right)\).
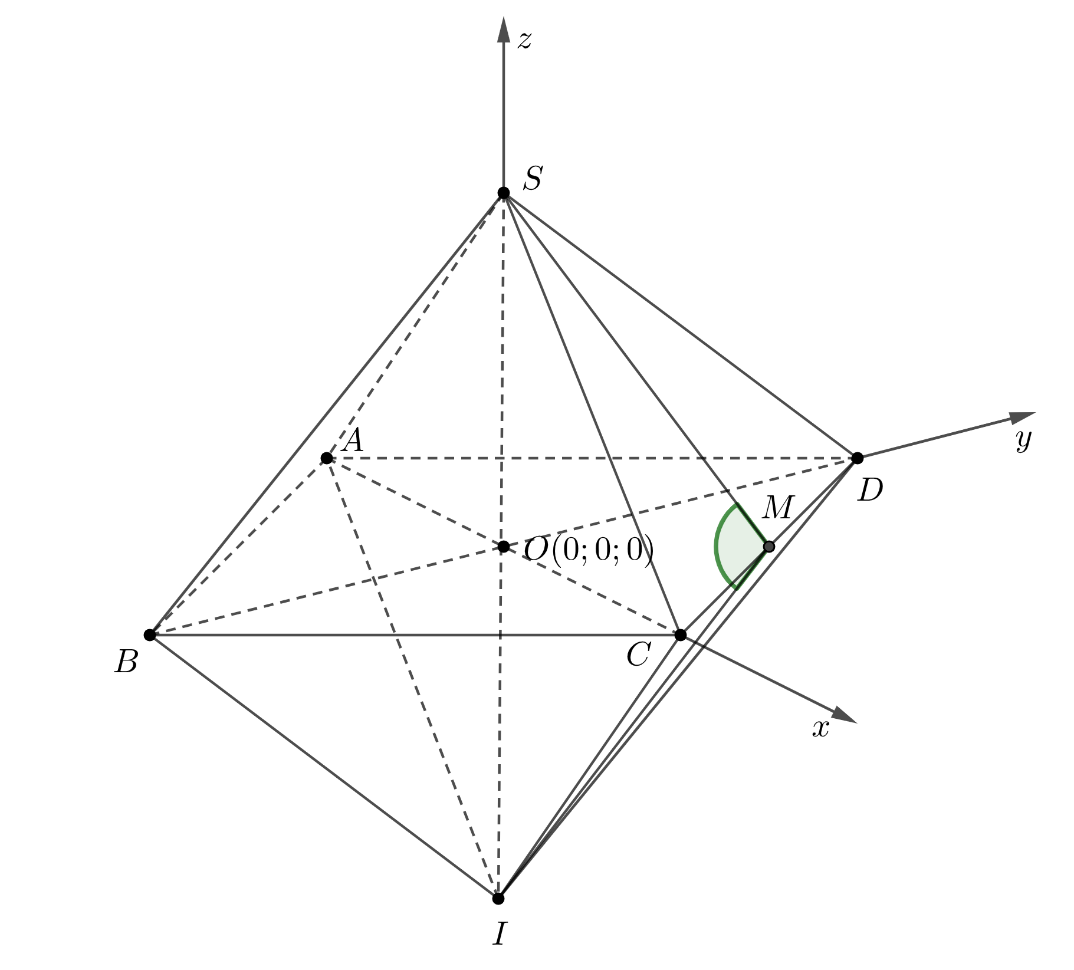
Có \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow \left[ {S;CD;I} \right] = \widehat {SMI}\).
Ta có \(\overrightarrow {MS} \left( { - \frac{1}{{2\sqrt 2 }}; - \frac{1}{{2\sqrt 2 }};\frac{1}{{\sqrt 2 }}} \right),\overrightarrow {MI} \left( { - \frac{1}{{2\sqrt 2 }}; - \frac{1}{{2\sqrt 2 }}; - \frac{1}{{\sqrt 2 }}} \right)\).
\[ \Rightarrow \cos \widehat {SMI} = \frac{{ - \frac{1}{{2\sqrt 2 }}. - \frac{1}{{2\sqrt 2 }} + - \frac{1}{{2\sqrt 2 }}. - \frac{1}{{2\sqrt 2 }} + \frac{1}{{\sqrt 2 }}. - \frac{1}{{\sqrt 2 }}}}{{\sqrt {{{\left( { - \frac{1}{{2\sqrt 2 }}} \right)}^2} + {{\left( { - \frac{1}{{2\sqrt 2 }}} \right)}^2} + {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}} .\sqrt {{{\left( { - \frac{1}{{2\sqrt 2 }}} \right)}^2} + {{\left( { - \frac{1}{{2\sqrt 2 }}} \right)}^2} + {{\left( {\frac{{ - 1}}{{\sqrt 2 }}} \right)}^2}} }} = - \frac{1}{3}\]
\[ \Rightarrow \widehat {SMI} \approx 109^\circ \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng.
b) Đúng.
Ta có: \(\overrightarrow {C'K} = \overrightarrow {C'C} + \overrightarrow {CK} = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CD} } \right) = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {C'A'} + \overrightarrow {C'D'} } \right)\)
\( = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {C'D'} } \right) = \overrightarrow {C'C} + \frac{1}{2}\overrightarrow {C'B'} + \overrightarrow {C'D'} \)
c) Sai.
Ta có: \[\overrightarrow {AB} .\overrightarrow {B'D'} = \left( {\overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {B'B} } \right).\overrightarrow {B'D'} = \overrightarrow {AA'} .\overrightarrow {B'D'} + \overrightarrow {A'B'} .\overrightarrow {B'D'} + \overrightarrow {B'B} .\overrightarrow {B'D'} = \overrightarrow {A'B'} .\overrightarrow {B'D'} \]
\( = A'B'.B'D'.{\rm{cos}}\left( {\overrightarrow {A'B'} ,\overrightarrow {B'D'} } \right) = a.a\sqrt 2 .{\rm{cos}}\left( {135^\circ } \right) = - {a^2}\)
d) Đúng.
Ta đặt \[\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \]. Ta có \[\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = \left| {\overrightarrow c } \right| = a\]
\[\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} \] hay \[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b + \overrightarrow c \]
Mặt khác
\[\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \left( {\overrightarrow {AB} + \overrightarrow {BN} } \right) - \left( {\overrightarrow {AD} + \overrightarrow {DM} } \right)\] với \[\overrightarrow {BN} = \frac{x}{a}.\overrightarrow a \] và \[\overrightarrow {DM} = \frac{x}{a}.\overrightarrow b \]
Do đó \[\overrightarrow {MN} = \left( {\overrightarrow b + \frac{x}{a}\overrightarrow a } \right) - \left( {\overrightarrow c + \frac{x}{a}\overrightarrow b } \right) = \frac{x}{a}\overrightarrow a + \left( {a - \frac{x}{a}} \right)\overrightarrow b - \overrightarrow c \]
Ta có \[\overrightarrow {AC'} .\overrightarrow {MN} = \left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\left[ {\frac{x}{a}\overrightarrow a + \left( {a - \frac{x}{a}} \right)\overrightarrow b - \overrightarrow c } \right]\]
Vì \[\overrightarrow a .\overrightarrow b = 0,\overrightarrow a .\overrightarrow c = 0,\overrightarrow b .\overrightarrow c = 0\] nên ta có
\[\overrightarrow {AC'} .\overrightarrow {MN} = \frac{x}{a}{\overrightarrow a ^2} + \left( {1 - \frac{x}{a}} \right){\overrightarrow b ^2} - {\overrightarrow c ^2} = x.a + \left( {1 - \frac{x}{a}} \right){a^2} - {a^2} = 0\], vậy góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng \(90^\circ \).
Câu 2
Lời giải
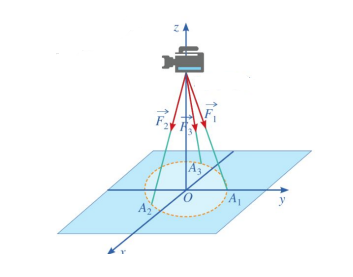
Ta có: \(\overrightarrow {E{A_1}} = \left( {0;1; - 8} \right)\),\(\overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\), \(\overrightarrow {E{A_3}} = \left( {\frac{{ - \sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\) Nên \(E{A_1} = E{A_2} = E{A_3} = \sqrt {65} \)
Mặt khác, \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) vì đèn cân bằng và trọng lực của đèn tác dụng đều lên 3 chân của giá đỡ
Do đó : \(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} = \left( {0;k; - 8k} \right)\),\[\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\],\(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} = \left( {\frac{{ - \sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\)
\( \Rightarrow {\overrightarrow F _1} + \overrightarrow {{F_2}} + {\overrightarrow F _3} = \left( {0;0; - 24k} \right)\)
Mà \({\overrightarrow F _1} + \overrightarrow {{F_2}} + {\overrightarrow F _3} = \overrightarrow P = \left( {0;0; - 240} \right) \Rightarrow - 24k = - 240 \Rightarrow k = 10\)
Vậy \(\overrightarrow {{F_1}} = \left( {0;10; - 80} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.