Một chiếc đèn chùm treo có khối lượng m = 5kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA,SB,SC,SD sao cho S.ABCD là hình chóp tứ giác đều có (Hình).
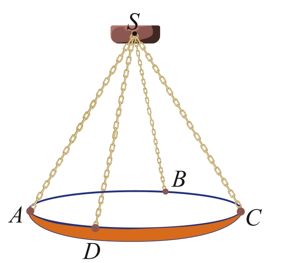
Biết \(\vec P = m\vec g\) trong đó \(\vec g\) là vectơ gia tốc rơi tự do có độ lớn \(10\;m/{s^2}\), \(\vec P\) là trọng lực tác động vật có đơn bị là \(N\), \(m\) là khối lượng của vật có đơn vị \(kg\). Cho các kết luận dưới đây.
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vec tơ đồng phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|.\)
c) Độ lớn của trọng lực \(\vec P\) tác động lên chiếc đèn chùm bằng \(50\;N.\)
d) Độ lớn của lực căng cho mỗi sợi xích bằng \(\frac{{25\sqrt 3 }}{6}\;N.\)
Số kết luận ĐÚNG là:
Biết \(\vec P = m\vec g\) trong đó \(\vec g\) là vectơ gia tốc rơi tự do có độ lớn \(10\;m/{s^2}\), \(\vec P\) là trọng lực tác động vật có đơn bị là \(N\), \(m\) là khối lượng của vật có đơn vị \(kg\). Cho các kết luận dưới đây.
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vec tơ đồng phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|.\)
c) Độ lớn của trọng lực \(\vec P\) tác động lên chiếc đèn chùm bằng \(50\;N.\)
d) Độ lớn của lực căng cho mỗi sợi xích bằng \(\frac{{25\sqrt 3 }}{6}\;N.\)
Số kết luận ĐÚNG là:
A. 1.
B. 2.
C. 3.
D. 0.
Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) Đúng |
b) Đúng |
c) Đúng |
d) Sai |
c) Độ lớn trọng lực tác động lên đèn chùm là: \(P = mg = 5.10 = 50\;N\)
d) Ta có \(S.ABCD\) là hình chóp tứ giác đều \( = > SA = SB = SC = SD\)
Mà = > \) Tam giác \[SAC\] đều
Gọi \[O\] là trung điểm \(AC\).
Ta có: Hợp lực của 4 sợi xích là: \(\vec F = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \)
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực hay \(4\overrightarrow {SO} = \vec P\) hay \(4SO = P \Leftrightarrow SO = 12,5\)
Xét tam giác đều \(SAC:SA = \frac{{\sqrt 3 }}{2}SO = \frac{{25\sqrt 3 }}{4}\)
Vậy độ lớn của lực căng cho mỗi sợi xích là \(\frac{{25\sqrt 3 }}{4}\;N.\)
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \(A\left( {1,5;1; - 0,5} \right)\) và \(C\left( {1;3;2} \right)\)
\(\overrightarrow {AC} \left( { - 0,5;2;2,5} \right)\)
Khi đó phương trình đường thẳng \(AC\) là\(\left\{ \begin{array}{l}x = - 0,5t + 1\\y = 2t + 3\\z = 2,5t + 2\end{array} \right.\) suy ra \(2,5t + 2 = 0 \Rightarrow t = - \frac{4}{5}\).
Khi đó \(\left\{ \begin{array}{l}x = \frac{7}{5}\\y = \frac{7}{5}\\z = 0\end{array} \right.\) hay \(B\left( {\frac{7}{5};\frac{7}{5};0} \right)\)
Lời giải
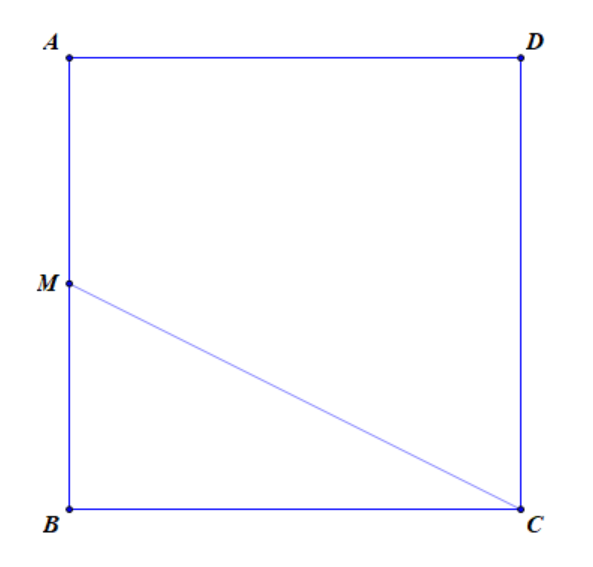
\(\overrightarrow {BD} = \left( { - 8; - 4; - 8} \right)\)\( \Rightarrow BD = 12\)\( \Rightarrow AB = \frac{{12}}{{\sqrt 2 }}\)\( = 6\sqrt 2 \).
Gọi \(M\)là trung điểm \(AB\)\( \Rightarrow MC = 3\sqrt {10} \).
\(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right|\)\( = \left| {2\overrightarrow {CM} } \right|\)\( = 2CM\)\( = 6\sqrt {10} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo