Cho 4 điểm \(A(1;2;0);B(5;1;4);C(7; - 2; - 2);D(3;m;2)\)

a) Độ dài đoạn \(AB\) lớn hơn độ dài đoạn \(AC\).

b) \(m = \frac{3}{2}\) thì \(D\) là trung điểm của \(AB\).

c) \(m = 5\) thì \(AB \bot AD\).

d) \(m =  - 1\) thì \(AB\)//\(CD\).

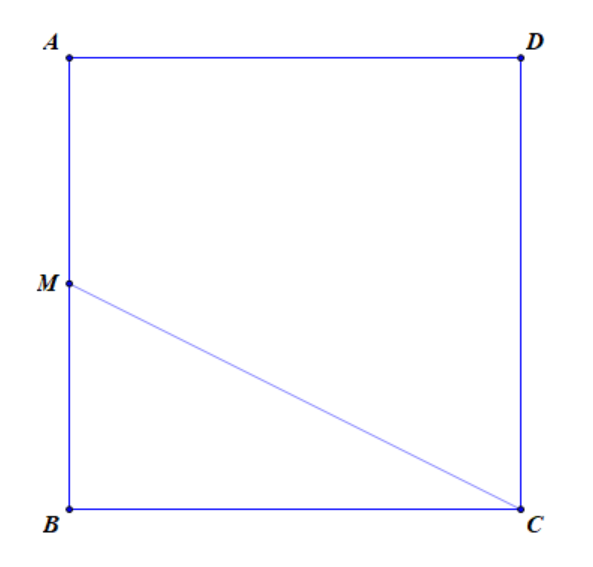
\(\overrightarrow {BD}  = \left( { - 8; - 4; - 8} \right)\)\( \Rightarrow BD = 12\)\( \Rightarrow AB = \frac{{12}}{{\sqrt 2 }}\)\( = 6\sqrt 2 \).

Gọi \(M\)là trung điểm \(AB\)\( \Rightarrow MC = 3\sqrt {10} \).

\(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right|\)\( = \left| {2\overrightarrow {CM} } \right|\)\( = 2CM\)\( = 6\sqrt {10} \).

Ta có: \(A\left( {1,5;1; - 0,5} \right)\) và \(C\left( {1;3;2} \right)\)

\(\overrightarrow {AC} \left( { - 0,5;2;2,5} \right)\)

Khi đó phương trình đường thẳng \(AC\) là\(\left\{ \begin{array}{l}x =  - 0,5t + 1\\y = 2t + 3\\z = 2,5t + 2\end{array} \right.\) suy ra \(2,5t + 2 = 0 \Rightarrow t =  - \frac{4}{5}\).

Khi đó \(\left\{ \begin{array}{l}x = \frac{7}{5}\\y = \frac{7}{5}\\z = 0\end{array} \right.\) hay \(B\left( {\frac{7}{5};\frac{7}{5};0} \right)\)