Cho hình lập phương ABCD.A'B'C'D'. Gọi \[O\] là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
Câu hỏi trong đề: Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 2 có đáp án !!
Quảng cáo
Trả lời:
Chọn B
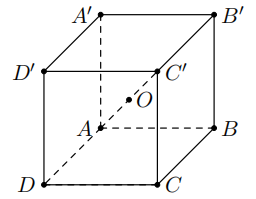
Ta có \[\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \].
Mặt khác \[O\] là trung điểm \[AC' \Rightarrow \overrightarrow {AO} = \frac{1}{2}\overrightarrow {AC'} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
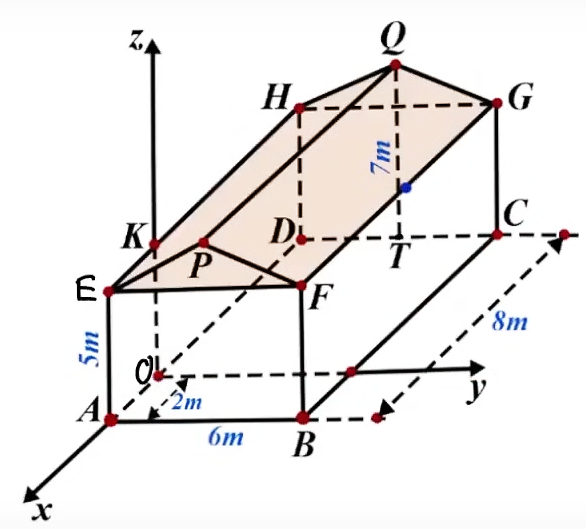
a) Sai. Máy bay đang di chuyển từ điểm \[M\left( {500;\,200;\,10} \right)\] đến điểm \[N\left( {800;\,300;\,10} \right)\]. Hoành độ \[x\] và tung \[y\] tăng lên, cao độ \[z\] không đổi. Máy bay đang di chuyển ra xa vị trí đặt ra đa.
b) Đúng. Ta có \[\overrightarrow {MN} \left( {300;\,100;\,0} \right)\] suy ra \(MN = \sqrt {{{300}^2} + {{100}^2} + {0^2}} = 100\sqrt {10} \,\,{\rm{km}}\).
c) Sai. 20 phút \( = \frac{1}{3}\) giờ.
Tốc độ của máy bay khi di chuyển từ \[M\] đến \[N\] là \[\frac{{100\sqrt {10} }}{{\frac{1}{3}}} = 300\sqrt {10} \,\,{\rm{km/h}}\].
d) Sai.

Trong 20 phút, máy bay di chuyển từ điểm \[M\left( {500;\,200;\,10} \right)\] đến điểm \[N\left( {800;\,300;\,10} \right)\].
Nếu giữ nguyên vận tốc và hướng bay thì sau 4 phút tiếp theo máy bay di chuyển đến vị trí điểm \(Q\left( {a;\,b;\,c} \right)\) sao cho \(\overrightarrow {NQ} = \frac{1}{5}\overrightarrow {MN} \).
Suy ra \(\left\{ \begin{array}{l}a - 800 = \frac{1}{5}.300\\b - 300 = \frac{1}{5}.100\\c - 10 = \frac{1}{5}.0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 860\\b = 320\\c = 10\end{array} \right. \Rightarrow Q\left( {860;\,320;\,10} \right)\). Vậy \[a + b + c = 1190\].
Lời giải
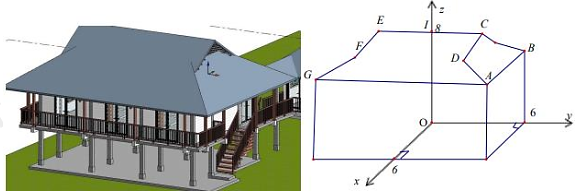
Ta có CDFE là hình chữ nhật và I là trung điểm của CE, nên F và D đối xứng nhau qua mặt phẳng \(\left( {Oxz} \right)\).
Có \(F\left( {4; - 4;7} \right)\), suy ra \(D\left( {4;4;7} \right)\).
Xét hình thang ADFG, có A đối xứng với G qua mặt \(\left( {Oxz} \right)\).
Có \(G\left( {6; - 6;6} \right)\), suy ra \(A\left( {6;6;6} \right)\).
Ta có điểm B nằm trên mặt phẳng \(\left( {Oyz} \right)\), tọa độ điểm \(B\left( {0;6;6} \right)\).
Suy ra \(\overrightarrow {AB} = \left( { - 6;0;0} \right)\) và \(\overrightarrow {DC} = \left( { - 1;0;1} \right)\), có:
\({\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DC} }}{{\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {DC} } \right|}} = \frac{6}{{\sqrt {{6^2}} .\sqrt {{1^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\).
Vậy góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {AB} \) bằng \(45^\circ \).
Đáp án: 45.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.