Hai dây dẫn thẳng dài đặt song song với nhau và cách nhau $4\ \text{cm}$. Điểm $M$ cách dây dẫn mang dòng điện $I_2$ $4\ \text{cm}$ như hình vẽ. Dòng điện chạy qua hai dây dẫn này có cùng cường độ là $5\ \text{A}$, nhưng ngược chiều nhau. Biết độ lớn cảm ứng từ do dòng điện $I$ chạy trong dây dẫn thẳng dài tạo ra tại vị trí cách dây dẫn một khoảng $r$ là $B = 2\cdot 10^{-7}\,\dfrac{I}{r}$, với $B$ tính bằng \textit{tesla} (T), $r$ tính bằng mét (m) và $I$ tính bằng \textit{ampe} (A). Độ lớn cảm ứng từ tổng hợp tại điểm $M$ bằng
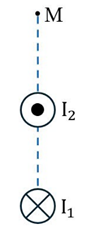
Hai dây dẫn thẳng dài đặt song song với nhau và cách nhau $4\ \text{cm}$. Điểm $M$ cách dây dẫn mang dòng điện $I_2$ $4\ \text{cm}$ như hình vẽ. Dòng điện chạy qua hai dây dẫn này có cùng cường độ là $5\ \text{A}$, nhưng ngược chiều nhau. Biết độ lớn cảm ứng từ do dòng điện $I$ chạy trong dây dẫn thẳng dài tạo ra tại vị trí cách dây dẫn một khoảng $r$ là $B = 2\cdot 10^{-7}\,\dfrac{I}{r}$, với $B$ tính bằng \textit{tesla} (T), $r$ tính bằng mét (m) và $I$ tính bằng \textit{ampe} (A). Độ lớn cảm ứng từ tổng hợp tại điểm $M$ bằng

Quảng cáo
Trả lời:
Đáp án đúng là D
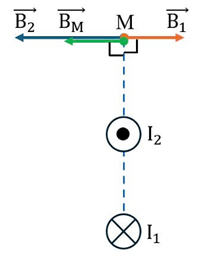
Cảm ứng từ tổng hợp tại $M$ có phương và chiều như hình vẽ.
Độ lớn cảm ứng từ tại $M$ do dòng điện $I_1$ và $I_2$ gây ra lần lượt là:
\[
B_1 = 2\cdot 10^{-7}\,\frac{I_1}{r_{1M}}
= 2\cdot 10^{-7}\,\frac{5}{0{,}08}
= 1{,}25\cdot 10^{-5}\ \text{(T)},
\]
\[
B_2 = 2\cdot 10^{-7}\,\frac{I_2}{r_{2M}}
= 2\cdot 10^{-7}\,\frac{5}{0{,}04}
= 2{,}5\cdot 10^{-5}\ \text{(T)}.
\]
Do $\vec B_1$ ngược hướng với $\vec B_2$ nên độ lớn cảm ứng từ tổng hợp tại $M$:
\[
B_M = \bigl|\,B_1 - B_2\,\bigr|
= \bigl|\,1{,}25\cdot 10^{-5} - 2{,}5\cdot 10^{-5}\,\bigr|
= 1{,}25\cdot 10^{-5}\ \text{T}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là B
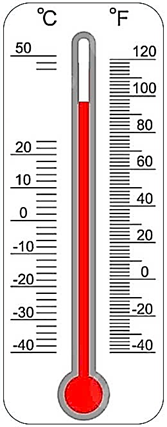
Vì thủy ngân giãn nở tuyến tính theo nhiệt độ, nên khi nhiệt độ tăng thêm $1^\circ\text{C}$ thì chiều dài cột thủy ngân tăng một đoạn
\[
\Delta \ell_{1^\circ\text{C}}=\frac{6{,}25}{50}=0{,}125\ \text{cm}.
\]
Khoảng cách từ vạch $0^\circ\text{C}$ đến mức thủy ngân là $4{,}5\ \text{cm}$, do đó nhiệt độ là
\[
t=\frac{4{,}5}{0{,}125}=36^\circ\text{C}.
\]
Câu 2
Lời giải
Đáp án đúng là B
Do nhiệt độ đo được là hàm bậc nhất theo chiều dài cột thủy ngân nên ta có: $t = a\,\ell + b$.
Khi $t = 0^\circ\text{C}$, $\ell = 2\ \text{cm}$:
\[
0 = a\cdot 2 + b \;\Leftrightarrow\; 2a + b = 0 \quad (1)
\]
Khi $t = 100^\circ\text{C}$, $\ell = 22\ \text{cm}$:
\[
100 = a\cdot 22 + b \;\Leftrightarrow\; 22a + b = 100 \quad (2)
\]
Từ (1) và (2) suy ra hệ:
\[
\begin{cases}
2a + b = 0,\\
22a + b = 100
\end{cases}
\Rightarrow a = 5,\quad b = -10.
\]
Vậy $t = 5\ell - 10$. Với $\ell = 18\ \text{cm}$:
\[
t = 5\cdot 18 - 10 = 80^\circ\text{C}.
\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. nhận một công bằng 270 J.
B. nhận một công bằng 70 J.
C. thực hiện một công bằng 70 J.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
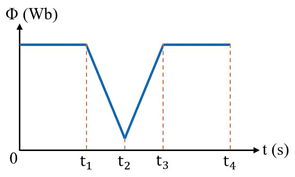
A. Từ t = 0 đến t = t2.
B. Từ t = t1 đến t = t2.
C. Từ t = t2 đến t = t4.
D. Từ t = 0 đến t = t1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.