Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên.
Trong mặt phẳng toạ độ \(Oxy\), chọn điểm có tọa độ \(\left( {O;{y_0}} \right)\) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: \(y = \frac{{ - g \cdot {x^2}}}{{2 \cdot v_0^2 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot x + {y_0}\); trong đó:
g là gia tốc trọng trường (thường được chọn là \(9,8\;m/{s^2}\) );
\(\alpha \) là góc phát cầu (so với phương ngang của mặt đất);
\({v_0}\) là vận tốc ban đầu của cầu;
\({y_0}\) là khoảng cách từ vị trí phát cầu đến mặt đất.
Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.
Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là \(6,68\;m\). Quan sát hình bên dưới, hỏi người chơi đã phát cầu góc khoảng bao nhiêu độ so với mặt đất? ( biết cầu rời mặt vợt ở độ cao \(0,7\;m\) so với mặt đất và vận tốc xuất phát của cầu là \(8\;m/s\), bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng).
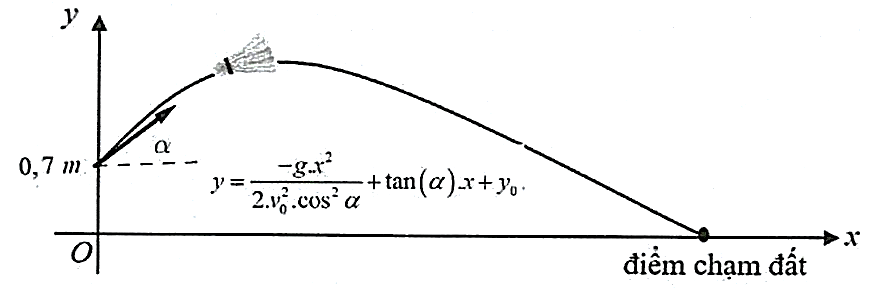
Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên.
Trong mặt phẳng toạ độ \(Oxy\), chọn điểm có tọa độ \(\left( {O;{y_0}} \right)\) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: \(y = \frac{{ - g \cdot {x^2}}}{{2 \cdot v_0^2 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot x + {y_0}\); trong đó:
g là gia tốc trọng trường (thường được chọn là \(9,8\;m/{s^2}\) );
\(\alpha \) là góc phát cầu (so với phương ngang của mặt đất);
\({v_0}\) là vận tốc ban đầu của cầu;
\({y_0}\) là khoảng cách từ vị trí phát cầu đến mặt đất.
Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.
Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là \(6,68\;m\). Quan sát hình bên dưới, hỏi người chơi đã phát cầu góc khoảng bao nhiêu độ so với mặt đất? ( biết cầu rời mặt vợt ở độ cao \(0,7\;m\) so với mặt đất và vận tốc xuất phát của cầu là \(8\;m/s\), bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng).
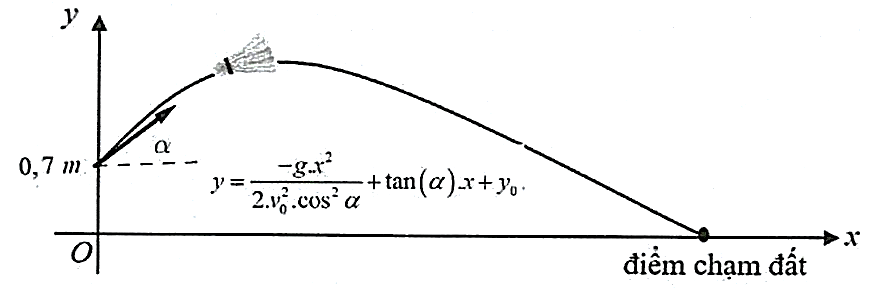
Câu hỏi trong đề: Đề kiểm tra Phương trình lượng giác cơ bản (có lời giải) !!
Quảng cáo
Trả lời:
Với \(g = 9,8\;m/{s^2}\), vận tốc ban đầu \({v_0} = 8\;m/s\), phương trình quỹ đạo của cầu:
\(y = \frac{{ - g \cdot {x^2}}}{{2 \cdot v_0^2 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot x + {y_0}\)
Khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là \(6,68\;m\); nghĩa là \(x = 6,68\;m\).
Vậy người chơi đã phát cầu một góc gần \({54^0}\) hoặc gần so với mặt đất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Sai |
b) Sai |
c) Đúng |
d) Đúng |
\(\sin 2x = - \frac{1}{2} \Leftrightarrow \sin 2x = \sin \frac{{ - \pi }}{6} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x = \frac{{ - \pi }}{6} + k2\pi }\\{2x = \frac{{7\pi }}{6} + k2\pi }\end{array}(k \in \mathbb{Z}) \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{ - \pi }}{{12}} + k\pi }\\{x = \frac{{7\pi }}{{12}} + k\pi }\end{array}(k \in \mathbb{Z})} \right.} \right.\).
\(0 < x < \pi \Rightarrow \left[ {\begin{array}{*{20}{l}}{0 < \frac{{ - \pi }}{{12}} + k\pi < \pi }\\{0 < \frac{{7\pi }}{{12}} + k\pi < \pi }\end{array}(k \in \mathbb{Z}) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{k = 1}\\{k = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{11\pi }}{{12}}}\\{x = \frac{{7\pi }}{{12}}}\end{array}} \right.} \right.\).
Lời giải
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
Ta có: \(2\sin x = \sqrt 2 \Leftrightarrow \sin x = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{4}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}(k \in \mathbb{Z}) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}(k \in \mathbb{Z}).} \right.} \right.\)
Vậy phương trình có nghiệm là: \(x = \frac{\pi }{4} + k2\pi ;x = \frac{{3\pi }}{4} + k2\pi (k \in \mathbb{Z})\).
Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{\pi }{4}\)
Số nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là một nghiệm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.