Số điểm một cầu thủ ghi được trong 20 trận đấu được cho ở bảng sau:
25
23
21
13
8
14
15
18
22
11
24
12
14
14
18
6
8
25
10
11
a) Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 14.{\rm{ }}\)
b) Tứ phân vị thứ ba của dãy số liệu là \({Q_3} = 11,5.{\rm{ }}\)
c) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
Điểm số
\([6;10)\)
\([11;15)\)
\([16;20)\)
\([21;25)\)
Số trận
4
8
2
6
d) Ứớc lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên ta được tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 8,25\).
Số điểm một cầu thủ ghi được trong 20 trận đấu được cho ở bảng sau:
|
25 |
23 |
21 |
13 |
8 |
14 |
15 |
18 |
22 |
11 |
|
24 |
12 |
14 |
14 |
18 |
6 |
8 |
25 |
10 |
11 |
a) Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 14.{\rm{ }}\)
b) Tứ phân vị thứ ba của dãy số liệu là \({Q_3} = 11,5.{\rm{ }}\)
c) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
|
Điểm số |
\([6;10)\) |
\([11;15)\) |
\([16;20)\) |
\([21;25)\) |
|
Số trận |
4 |
8 |
2 |
6 |
d) Ứớc lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên ta được tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 8,25\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
a) b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
\(6;8;8;10;11;11;12;13;14;14;14;15;18;18;21;22;23;24;25;25\)
Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = \frac{{14 + 14}}{2} = 14.{\rm{ }}\)
Tứ phân vị thứ nhất của dãy số liệu \(6;8;8;10;11;11;12;13;14;14\);
\({Q_1} = \frac{{11 + 11}}{2} = 9,05.{\rm{ }}\)
Tứ phân vị thứ ba của dãy số liệu \(14;15;18;18;21;22;23;24;25;25\)
\({Q_3} = \frac{{21 + 22}}{2} = 21,5.{\rm{ }}\)
c)
|
Điểm số |
\([6;10)\) |
\([11;15)\) |
\([16;20)\) |
\([21;25)\) |
|
Số trận |
4 |
8 |
2 |
6 |
d) Vì số trận là số nguyên nên ta hiệu chỉnh lại bảng số liệu sau:
|
Điểm số |
\([5,5;10,5)\) |
\([10,5;15,5)\) |
\([15,5;20,5)\) |
\([20,5;25,5)\) |
|
Số trận |
4 |
8 |
2 |
6 |
Gọi \({x_1};{x_2}; \ldots ;{x_{20}}\) lần lượt là số điểm ghi được ở mỗi trận đấu xếp theo thứ tự không giảm.
Do \({x_1}; \ldots ;{x_4} \in [5,5;10,5);{x_5}; \ldots ;{x_{12}} \in [10,5;15,5);{x_{13}},{x_{14}} \in [15,5;20,5);{x_{15}}; \ldots ;{x_{20}} \in [20,5;25,5)\) nên trung vị của mẫu số liệu \({x_1}; \ldots ;{x_{20}}\) là \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) \in [10,5;15,5)\).
Ta xác định được \(n = 20,{n_m} = 8,C = 4,{u_m} = 10,5;{u_{m + 1}} = 15,5\).
Suy ra tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}(15,5 - 10,5) = 14,25\).
Tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Do \({x_5},{x_6} \in [10,5;15,5)\) nên tứ phân vị thứ nhất của mẫu số liệu nhóm là: \({Q_1} = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}(15,5 - 10,5) = 11,125\).
Tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Do \({x_{15}},{x_{16}} \in [20,5;25,5)\) nên tứ phân vị thứ ba của mẫu số liệu nhóm là: \({Q_3} = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}(25,5 - 20,5) = 21,3\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Đúng |
b) Sai |
c) Đúng |
d) Đúng |
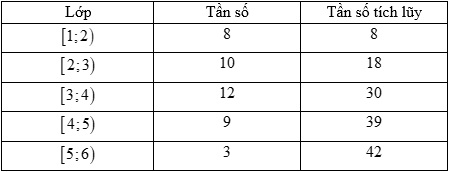
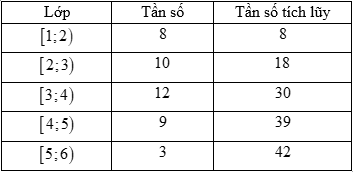
Cỡ mẫu của mẫu số liệu là \(n = 61\).
Gọi \({x_1},{x_2}, \ldots ,{x_{61}}\) là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Trung vị của mẫu số liệu này là \({x_{31}} \in [30;35)\).
Ta có: \({n_m} = 26;{C_1} = 4 + 12 = 16;{u_m} = 30;{u_{m + 1}} = 35\).
Tứ phân vị thứ hai chính là trung vị của mẫu số liệu ghép nhóm là:
\({Q_2} = {M_e} = 30 + \frac{{\frac{{61}}{2} - 16}}{{26}}(35 - 30) = \frac{{1705}}{{52}} \approx 32,79(\;cm){\rm{. }}\)
Xét nửa mẫu số liệu bên trái \({x_1},{x_2}, \ldots ,{x_{30}}\) có trung vị \(\frac{{{x_{15}} + {x_{16}}}}{2} \in [25;30)\).
Ta có: \({n_i} = 12;{C_1} = 4;{x_i} = 25;{x_{i + 1}} = 30\).
Suy ra tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = 25 + \frac{{\frac{{61}}{4} - 4}}{{12}}(30 - 25) = \frac{{475}}{{16}} \approx 29,69(\;cm)\).
Xét nửa mẫu số liệu bên trái \({x_{32}},{x_{33}}, \ldots ,{x_{61}}\) có trung vị \(\frac{{{x_{46}} + {x_{47}}}}{2} \in [35;40)\).
Ta có: \({n_j} = 13;{C_3} = 4 + 12 + 26 = 42;{x_i} = 35;{x_{i + 1}} = 40\).
Suy ra tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = 35 + \frac{{\frac{{3.61}}{4} - 42}}{{13}}(40 - 35) = \frac{{1895}}{{52}} \approx 36,44(\;cm)\).
Vậy các tứ phân vị của mẫu số liệu ghép nhóm là:
\({Q_1} \approx 29,69;{Q_2} = 32,79;{Q_3} = 36,44.{\rm{ }}\)
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
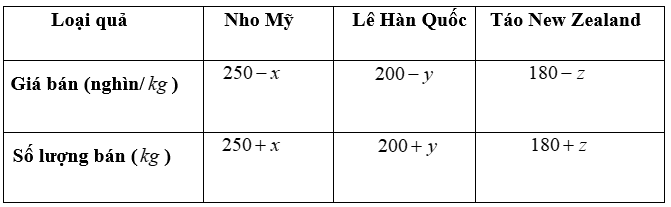
Vì số lượng hoa quả bán được là \(250 + x + 200 + y + 180 + z = 750\)là cố định nên bình quân mỗi \(kg\)hoa quả có giá cao nhất khi số tiền thu được là cao nhất.
Gọi \(P\) là tổng số tiền thu được.
Khi đó \(P = \left( {250 - x} \right)(250 + x) + (200 - y)(200 + y) + (180 - z)(180 + z)\)
\( = {250^2} - {x^2} + {200^2} - {y^2} + {180^2} - {z^2}\)=\(134900 - {x^2} - {y^2} - {z^2}\).
Ta có bất đẳng thức: \[{x^2} + {y^2} + {z^2} \ge \frac{1}{3}{\left( {x + y + z} \right)^2} = 4800\].
Do đó \(P \le 130100\).
Vậy \(P\) lớn nhất \( \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 120\\x = y = z\end{array} \right.\)\( \Leftrightarrow x = y = z = 40\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập