Phần 2. Trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

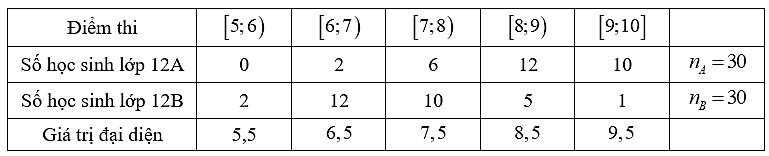
Thống kê điểm thi khảo sát đầu năm môn Toán của hai lớp 12A và 12B, ta thu được kết quả sau:

a) Từ khoảng biến thiên của điểm thi của học sinh hai lớp 12A và 12B, điểm thi khảo sát môn Toán của lớp 12A phân tán hơn của lớp 12B.

b) Số điểm trung bình môn Toán trong bài khảo sát đầu năm của lớp 12B lớn hơn của lớp 12A.

c) Khoảng tứ phân của lớp 12A lớn hơn 1.

d) Khoảng tứ phân vị của lớp 12A lớn hơn so với lớp 12B.

Khoảng biến thiên của điểm thi của học sinh hai lớp 12B là \({R_B} = 10 - 5 = 5\).

Vì \({R_B} > {R_A}\) nên điểm thi khảo sát môn Toán của lớp 12B phân tán hơn của lớp 12A.

b) Sai. Điểm trung bình môn Toán trong kỳ khảo sát của lớp 12A là :

\({\overline x _A} = \frac{{2.6,5 + 6.7,5 + 12.8,5 + 10.9,5}}{{30}} = \frac{{17}}{2} = 8,5\).

Số điểm trung bình môn Toán trong kỳ khảo sát của lớp 12B là :

\({\overline x _B} = \frac{{2.5,5 + 12.6,5 + 10.7,5 + 5.8,5 + 1.9,5}}{{30}} = \frac{{36}}{5} = 7,2\).

Vì \({\bar x_A} > {\bar x_B}\) nên số điểm trung bình môn Toán trong kỳ kiểm tra đánh giá của lớp 12A lớn hơn của lớp 12B.

c) Đúng. Lớp A có ta có: \(\frac{n}{4} = 7,5\,\,;\,\,\frac{n}{2} = 15;\,\,\frac{{3n}}{4} = 22,5\).

$Q_1=7+\frac{\frac{30}{4}-2}{8}.1=\frac{123}{16}\approx 7,69;Q_3=9+\frac{\frac{90}{4}-20}{30}.1=\frac{109}{12}\approx 9,08\Rightarrow {△}_Q=Q_3-Q_1=\frac{325}{36}\approx 1,34$.

d) Đúng. Lớp B có ta có: \(\frac{n}{4} = 7,5\,\,;\,\,\frac{n}{2} = 15;\,\,\frac{{3n}}{4} = 22,5\).