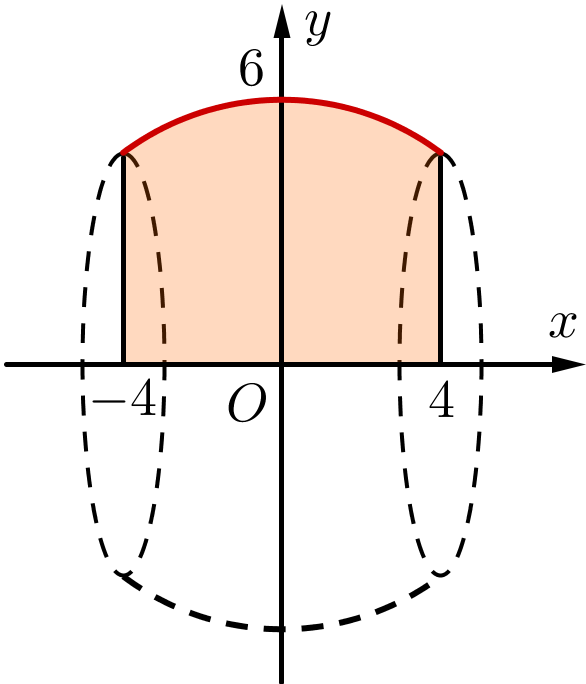
Người ta chế tác một giọt nước bằng thủy tinh. Biết giọt nước thủy tinh này là vật thể tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \[f\left( x \right) = \left\{ \begin{array}{l}\sqrt {4 - {x^2}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( { - 2 \le x \le 0,6} \right)\\ - \frac{{\sqrt {91} }}{{20}}x + \frac{{23\sqrt {91} }}{{100}}\,\,\,\,\left( {0,6 < x \le 4,6} \right)\end{array} \right.\] và trục \[Ox\] quanh trục \[Ox\] (đơn vị trên trục là centimet).
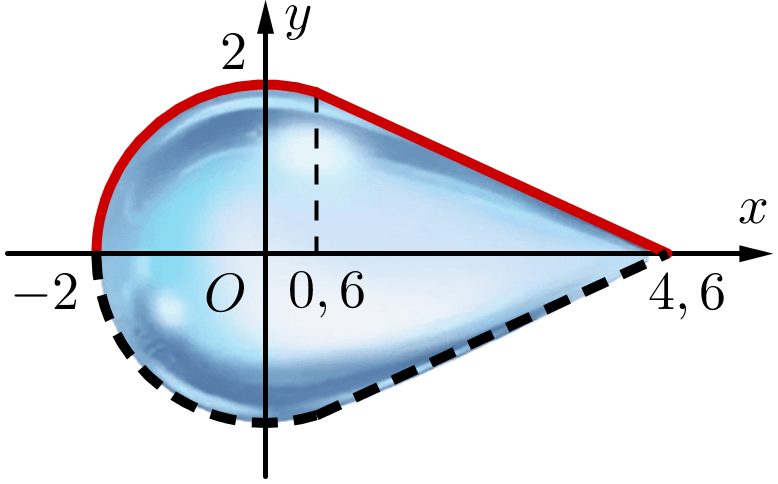
a) Hàm số \[y = f\left( x \right)\] liên tục tại \[x = 0,6\].
b) Diện tích mặt cắt của giọt nước thủy tinh khi cắt bởi mặt phẳng qua trục được tính bởi công thức \[S = 2\int\limits_{ - 2}^{4,6} {f\left( x \right){\rm{d}}x} \] cm2.
c) Thể tích của giọt nước thủy tinh này lớn hơn 40 cm3.
d) Biết khối lượng riêng của thủy tinh là \[\rho = 2,6\] g/cm3, khối lượng của giọt nước thủy tinh này là 102,22 g (làm tròn kết quả đến hàng phần trăm).
Người ta chế tác một giọt nước bằng thủy tinh. Biết giọt nước thủy tinh này là vật thể tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \[f\left( x \right) = \left\{ \begin{array}{l}\sqrt {4 - {x^2}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( { - 2 \le x \le 0,6} \right)\\ - \frac{{\sqrt {91} }}{{20}}x + \frac{{23\sqrt {91} }}{{100}}\,\,\,\,\left( {0,6 < x \le 4,6} \right)\end{array} \right.\] và trục \[Ox\] quanh trục \[Ox\] (đơn vị trên trục là centimet).

a) Hàm số \[y = f\left( x \right)\] liên tục tại \[x = 0,6\].
b) Diện tích mặt cắt của giọt nước thủy tinh khi cắt bởi mặt phẳng qua trục được tính bởi công thức \[S = 2\int\limits_{ - 2}^{4,6} {f\left( x \right){\rm{d}}x} \] cm2.
c) Thể tích của giọt nước thủy tinh này lớn hơn 40 cm3.
d) Biết khối lượng riêng của thủy tinh là \[\rho = 2,6\] g/cm3, khối lượng của giọt nước thủy tinh này là 102,22 g (làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
a) Đúng. \(\mathop {\lim }\limits_{x \to 0,{6^ - }} f\left( x \right) = \sqrt {4 - {{\left( {0,6} \right)}^2}} = \sqrt {4 - 0,36} = \sqrt {3,64} \approx 1,907\);
\(\mathop {\lim }\limits_{x \to 0,{6^ + }} f\left( x \right) = - \frac{{\sqrt {91} }}{{20}}.0,6 + \frac{{23\sqrt {91} }}{{100}} \approx 1,907\).
Vậy hàm số \(y = f\left( x \right)\) liên tục tại \(x = 0,6\).
b) Đúng. Diện tích mặt cắt của giọt nước thủy tinh khi cắt bởi mặt phẳng qua trục được tính bởi công thức \[S = 2\int\limits_{ - 2}^{4,6} {f\left( x \right){\rm{d}}x} \] cm2.
c) Sai. Thể tích của giọt nước thủy tinh này là:
\[V = {V_1} + {V_2} = \pi \int\limits_{ - 2}^{0,6} {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}{\rm{d}}x + } \,\pi \int\limits_{0,6}^{4,6} {{{\left( { - \frac{{\sqrt {91} }}{{20}}x + \frac{{23\sqrt {91} }}{{100}}} \right)}^2}{\rm{d}}x} = \frac{{4693\pi }}{{375}} \approx 39,32\] cm3.
d) Đúng. Khối lượng của giọt nước thủy tinh này là: \(m = \rho .V = 2,6.\frac{{4693\pi }}{{375}} \approx 102,22\)g.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Sai. Ta có: \(\int {\left( {{t^2} - 8t} \right){\rm{d}}t} = \frac{{{t^3}}}{3} - 4{t^2} + C\).
b) Sai. Ta có: \(f'\left( t \right) > 0\,\,\)khi \(8 < t < 10\) và \(f'\left( t \right) < 0\,\,\)khi \(3 < t < 8\).
Nên số lượng vi sinh vật giảm trong khoảng từ 3 giờ đến 8 giờ, sau đó tăng dần trong khoảng 8 giờ đến 10 giờ.
c) Đúng. Bảng biến thiên của \(f\left( t \right)\):
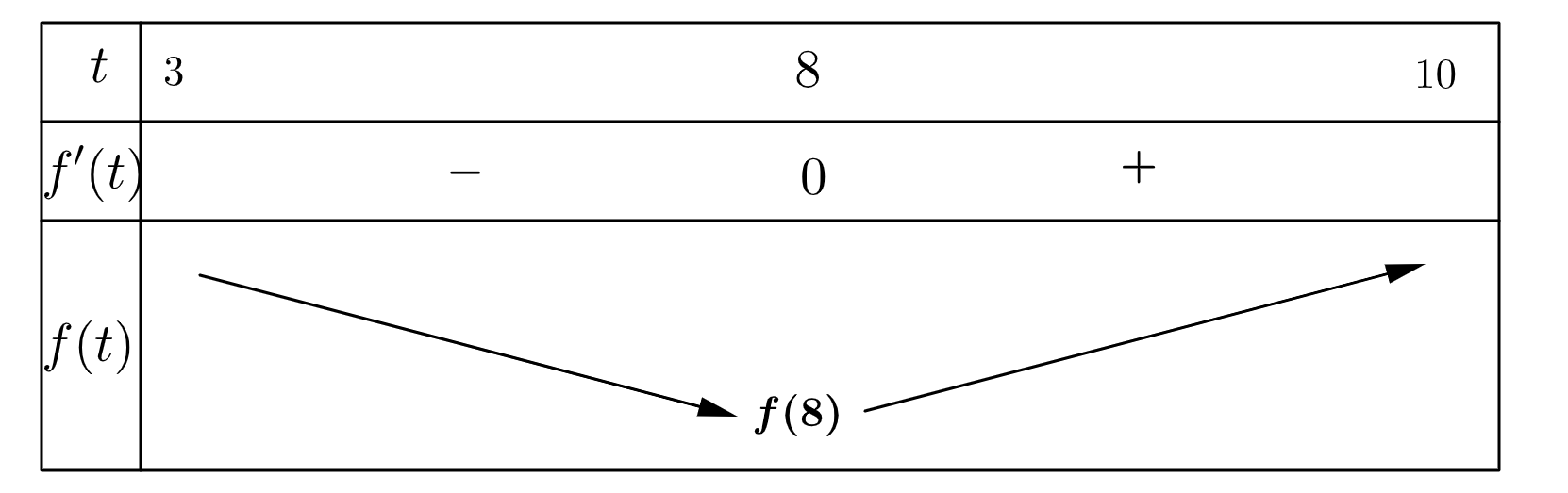
d) Đúng. \(f\left( t \right) = \frac{{{t^3}}}{3} - 4{t^2} + C\). Do \(f\left( 3 \right) = 50 \Rightarrow \frac{{{3^3}}}{3} - {4.3^2} + C = 50 \Rightarrow C = 77\).
Suy ra \(f\left( t \right) = \frac{1}{3}{t^3} - 4{t^2} + 77 \Rightarrow f\left( 6 \right) = 5\).
Lời giải
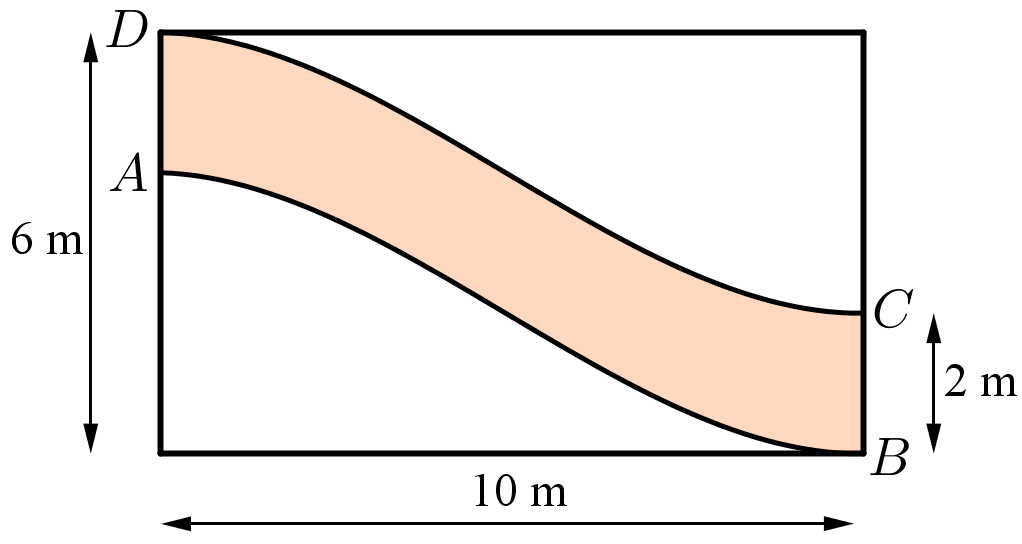
Để tính diện tích phần đổ bê tông, ta cần xác định diện tích giữa hai đường cong \(AB\) và \(DC\)
Đường cong DC là kết quả của việc tịnh tiến đường cong \(AB\) lên trên \(2\)m.
Giả sử hàm số của đường cong \(AB\) là \(f\left( x \right)\) thì hàm số của đường cong \(DC\) là \(f\left( x \right) + 2\).
Diện tích hình phẳng giới hạn bởi hai đường cong là: \[S = \int\limits_0^{10} {\left[ {f\left( x \right) + 2 - f\left( x \right)} \right]} {\rm{d}}x = 20\,{{\rm{m}}^2}\].
Lớp bê tông có độ dày là \(15\)cm tức là \(0,15\)m thì có thể tích là: \(20.0,15 = 3{{\rm{m}}^3}\).
Chi phí tổng cộng để đổ bê tông con đường đó là: \(3.1\,080\,000 = 3\,240\,000\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.