Phần 3. Trắc nghiệm trả lời ngắn
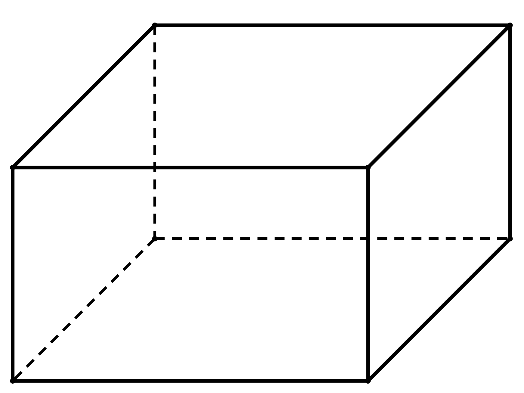
Hình dưới đây là mương dẫn nước thủy lợi tại một địa phương phục vụ tưới tiêu cho ruộng đồng. Phần không gian trong mương để nước chảy có mặt cắt ngang là hình chữ nhật \(ABCD\). Với điều kiện lưu lượng nước qua mương cho phép thì diện tích mặt cắt \(ABCD\) là \(0\,,48\,{{\rm{m}}^2}\). Để đảm bảo yêu cầu kỹ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài \(T = AB + \,BC + CD\) là ngắn nhất. Khi đó chiều rộng đáy mương bằng bao nhiêu mét (biết chiều rộng phải dưới 1 m, làm tròn kết quả đến hàng phần trăm)?


Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
Đặt \(BC = x\,\left( {\rm{m}} \right)\,\)với \(0 < x < 1\).
Theo đề bài ta có : \(AB.BC = 0\,,48 \Rightarrow AB = \frac{{0\,,48}}{{BC}} = \frac{{0\,,48}}{x}\).
Xét hàm số \(T = f\left( x \right) = AB + \,BC + CD = x + 2.AB = x + \frac{{0\,,96}}{x}\).
Đạo hàm \(f'\left( x \right) = 1 - \frac{{0\,,96}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 0\,,96 = 0 \Leftrightarrow x = \frac{{2\sqrt 6 }}{5} \simeq 0,98\,\left( {\rm{m}} \right)\).
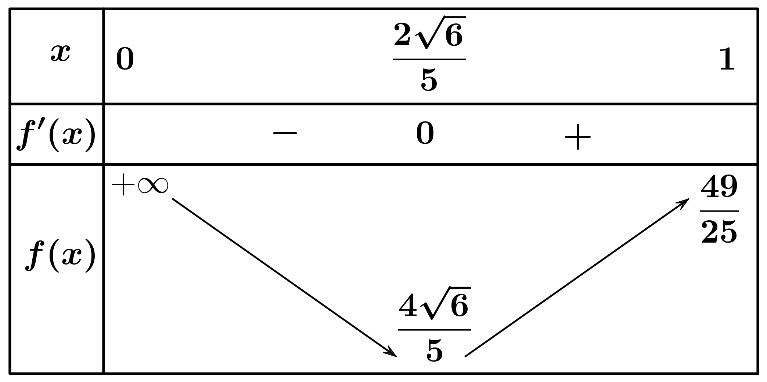
Vậy chiều rộng đáy mương \(BC = 0,98\,\left( {\rm{m}} \right)\,\)thỏa mãn yêu cầu bài toán.
Đáp án: 0,98.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện \(\left\{ \begin{array}{l}x > 0\\1700 - 7x > 0\end{array} \right. \Leftrightarrow 0 < x < \frac{{1700}}{7}\).
Doanh thu được khi công ty sản xuất và tiêu thụ hết \(x\) sản phẩm là \(R\left( x \right) = xp\left( x \right) = 1700x - 7{x^2}\).
Do đó, lợi nhuận thu được là
\(P\left( x \right) = xp\left( x \right) - C\left( x \right)\)\( = 1700x - 7{x^2} - \left( {16\,000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\)
\(P\left( x \right) = - 0,004{x^3} - 5,4{x^2} + 1200x - 16\,000\), \(0 < x < \frac{{1700}}{7}\).
\(P'\left( x \right) = - 0,012{x^2} - 10,8x + 1200\); \(P'\left( x \right) = 0 \Leftrightarrow - 0,012{x^2} + 10,8x + 1200 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1000\\x = 100\end{array} \right.\).
Đối chiếu điều kiện ta có \(x = 100\).
Lập bảng biến thiên của hàm số, ta thu được kết quả là
\(\mathop {\max }\limits_{\left( {0;\frac{{1700}}{7}} \right)} P\left( x \right) = P\left( {100} \right) = 46\,000\) (nghìn đồng).
Vậy công ty cần sản xuất 100 sản phẩm thì lợi nhuận thu được là cao nhất.
Đáp án: 100.
Câu 2
\(\left( {0; + \infty } \right)\).
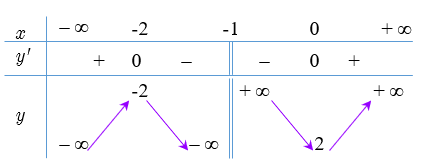
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - 2; - 1} \right)\).
Lời giải
Chọn D
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên các khoảng \(\left( { - 2; - 1} \right)\) và \(\left( { - 1;0} \right)\).
Vậy chọn đáp án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
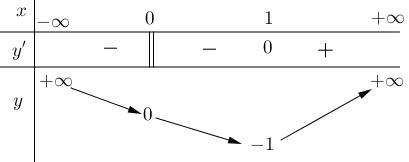
Hàm số có giá trị cực tiểu bằng \( - 1\).
Hàm số có giá trị nhỏ nhất bằng \( - 1\).
Hàm số có đúng một cực trị.
Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.