Cho hình hộp \[ABCD.A'B'C'D'\]. Đặt \[\overrightarrow {AB} = \overrightarrow a \], \[\overrightarrow {AD} = \overrightarrow b \], \[\overrightarrow {AA'} = \overrightarrow c \]. Phân tích vectơ \[\overrightarrow {AC'} \] theo \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] ta được
\[\overrightarrow {AC'} = - \overrightarrow a + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b - \overrightarrow c \].
\[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c \].
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 2 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng: C
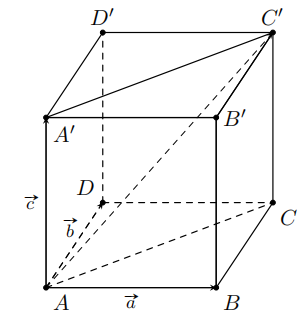
Ta có \[\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AC} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow a + \overrightarrow b + \overrightarrow c \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
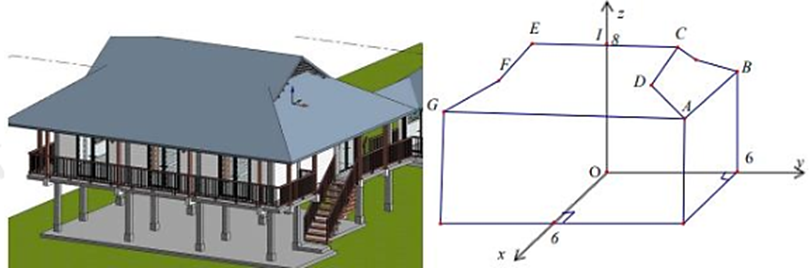
Ta có CDFE là hình chữ nhật và I là trung điểm của CE, nên F và D đối xứng nhau qua mặt phẳng \(\left( {Oxz} \right)\).
Có \(F\left( {4; - 4;7} \right)\), suy ra \(D\left( {4;4;7} \right)\).
Xét hình thang ADFG, có A đối xứng với G qua mặt \(\left( {Oxz} \right)\).
Có \(G\left( {6; - 6;6} \right)\), suy ra \(A\left( {6;6;6} \right)\).
Ta có điểm B nằm trên mặt phẳng \(\left( {Oyz} \right)\), tọa độ điểm \(B\left( {0;6;6} \right)\).
Suy ra \(\overrightarrow {AB} = \left( { - 6;0;0} \right)\) và \(\overrightarrow {DC} = \left( { - 1;0;1} \right)\), có:
\({\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DC} }}{{\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {DC} } \right|}} = \frac{6}{{\sqrt {{6^2}} .\sqrt {{1^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\).
Vậy góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {AB} \) bằng \(45^\circ \).
Đáp án: 45.
Lời giải
Chọn hệ trục như hình vẽ.
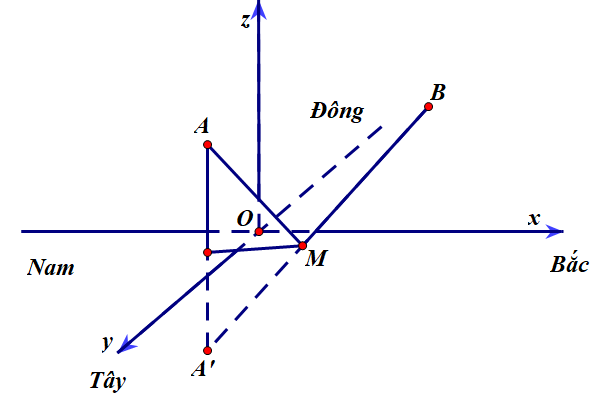
Gọi vị trí của hai chiếc drone lần lượt là \(A\left( { - 2,5; - 1,5;0,06} \right)\), \(B\left( {3;2,5;0,04} \right)\), \(M\left( {a;b;0} \right) \in \left( {Oxy} \right)\) là vị trí tiếp nhiên liệu cần tìm. Do \(A,B\) nằm cùng phía so với mặt phẳng \(Oxy\), ta gọi điểm đối xứng với \(A\) qua \(Oxy\) là \(A'\left( { - 2,5; - 1,5; - 0,06} \right)\).
Khi đó \(AM + BM = A'M + BM \ge A'B\).
Dấu “=” xảy ra khi và chỉ khi \(A',M,B\) thẳng hàng theo thứ tự đó
\( \Leftrightarrow \)\(\overrightarrow {A'B} = \left( {5,5;4;0,1} \right);\overrightarrow {BM} = \left( {a - 3;b - 2,5; - 0,04} \right)\) cùng phương.
Suy ra \(\frac{{a - 3}}{{5,5}} = \frac{{b - 2,5}}{4} = \frac{{ - 0,04}}{{0,1}} \Leftrightarrow a = 0,8;b = 0,9 \Rightarrow a + b = 1,7.\)
Đáp án: 1,7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(\left( {3\,;\,4\,;\,0} \right)\).
\(\left( {1\,;\, - 2\,;\, - 2} \right)\).
\(\left( {4\,;\,7\,;\,1} \right)\).
\(\left( {5\,;\,5\,;\, - 1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.