Cơn bão Yagi gây thiệt hại nghiêm trọng về người và tài sản cho nước ta, trong đó nặng nề nhất là tại thôn Làng Nủ, xã Phúc Khánh, huyện Bảo Yên, tỉnh Lào Cai, lũ quét và sạt lở đất đã vùi lấp 40 ngôi nhà. Cả nước đã chung tay ủng hộ và xây dựng lại nhà sàn cho người dân Làng Nủ theo thiết kế như hình vẽ dưới đây.
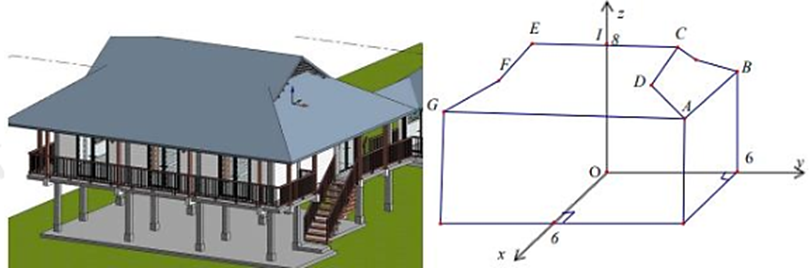
Giả sử áp dụng hệ trục tọa độ \(Oxyz\) như hình vẽ (đơn vị trên các trục là mét). Xét một bên của mái nhà gồm có một hình chữ nhật CDFE và một hình thang ADFG với các điểm \(G\left( {6; - 6;6} \right);C\left( {3;4;8} \right);F\left( {4; - 4;7} \right)\) và điểm \(I\) là trung điểm CE.
Biết góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {AB} \) bằng \(a^\circ \). Tìm a (kết quả làm tròn đến hàng đơn vị).
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 2 có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
Ta có CDFE là hình chữ nhật và I là trung điểm của CE, nên F và D đối xứng nhau qua mặt phẳng \(\left( {Oxz} \right)\).
Có \(F\left( {4; - 4;7} \right)\), suy ra \(D\left( {4;4;7} \right)\).
Xét hình thang ADFG, có A đối xứng với G qua mặt \(\left( {Oxz} \right)\).
Có \(G\left( {6; - 6;6} \right)\), suy ra \(A\left( {6;6;6} \right)\).
Ta có điểm B nằm trên mặt phẳng \(\left( {Oyz} \right)\), tọa độ điểm \(B\left( {0;6;6} \right)\).
Suy ra \(\overrightarrow {AB} = \left( { - 6;0;0} \right)\) và \(\overrightarrow {DC} = \left( { - 1;0;1} \right)\), có:
\({\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DC} }}{{\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {DC} } \right|}} = \frac{6}{{\sqrt {{6^2}} .\sqrt {{1^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\).
Vậy góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {AB} \) bằng \(45^\circ \).
Đáp án: 45.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn hệ trục như hình vẽ.
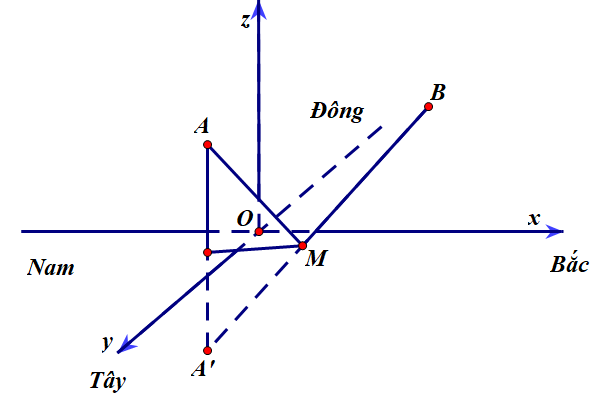
Gọi vị trí của hai chiếc drone lần lượt là \(A\left( { - 2,5; - 1,5;0,06} \right)\), \(B\left( {3;2,5;0,04} \right)\), \(M\left( {a;b;0} \right) \in \left( {Oxy} \right)\) là vị trí tiếp nhiên liệu cần tìm. Do \(A,B\) nằm cùng phía so với mặt phẳng \(Oxy\), ta gọi điểm đối xứng với \(A\) qua \(Oxy\) là \(A'\left( { - 2,5; - 1,5; - 0,06} \right)\).
Khi đó \(AM + BM = A'M + BM \ge A'B\).
Dấu “=” xảy ra khi và chỉ khi \(A',M,B\) thẳng hàng theo thứ tự đó
\( \Leftrightarrow \)\(\overrightarrow {A'B} = \left( {5,5;4;0,1} \right);\overrightarrow {BM} = \left( {a - 3;b - 2,5; - 0,04} \right)\) cùng phương.
Suy ra \(\frac{{a - 3}}{{5,5}} = \frac{{b - 2,5}}{4} = \frac{{ - 0,04}}{{0,1}} \Leftrightarrow a = 0,8;b = 0,9 \Rightarrow a + b = 1,7.\)
Đáp án: 1,7.
Lời giải
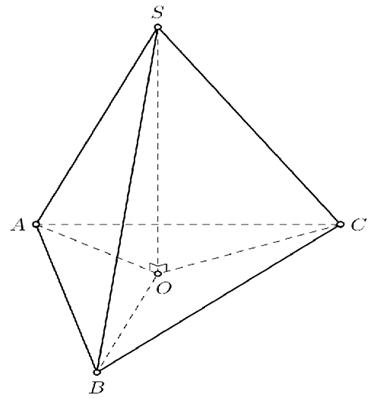
Biết ba sợi dây được thắt một đầu bên trên là điểm \(S\), ba sợi dây đỡ giá gỗ tại 3 điểm tạo thành tam giác đều \(ABC\), độ dài sợi dây \(SA = SB = SC = 60\,\left( {{\rm{cm}}} \right)\), bán kính hình tròn\(OA = OB = OC = 20\,\left( {{\rm{cm}}} \right)\).
Ta có hình chóp tam giác đều \(S.ABC\), gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
\( \Rightarrow SO \bot (ABC)\) và \(SO = \sqrt {S{A^2} - O{A^2}} = 40\sqrt 2 \left( {{\rm{cm}}} \right)\).
Gọi lực chịu đựng của mỗi sợi dây là \({T_1},\;T{}_2,{T_3}\)các lực này bằng nhau và không quá 15 N\( \Rightarrow {T_1} = {T_2} = {T_3} \le 15{\rm{N}}\)\( \Rightarrow \left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| \le 15\,{\rm{N}}\).
Lại có \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OB} + \overrightarrow {SO} + \overrightarrow {OC} = 3\overrightarrow {SO} \).
Gọi \(P\)là lực tác động lên miếng kê (là tổng lực của miếng giá gỗ hình tròn và lực của các chậu hoa) nên \(P = \left| {3\overrightarrow {SO} } \right| = 3SO\).
Vì \(P\)chia đều ra ba sợi dây
\( \Rightarrow \frac{P}{{3{T_1}}} = \frac{{3SO}}{{3SA}} = \frac{{SO}}{{SA}} = \frac{{40\sqrt 2 }}{{60}} = \frac{{2\sqrt 2 }}{3} \Leftrightarrow {T_1} = \frac{P}{{2\sqrt 2 }} \le 15{\rm{N}} \Leftrightarrow P \le 30\sqrt 2 {\rm{N}}\).
Suy ra trọng lượng của các chậu hoa là \({P_{hoa}} + {P_{go}} \le 30\sqrt 2 N \Leftrightarrow {P_{hoa}} \le \left( {30\sqrt 2 - 5} \right)N \approx 37,4{\rm{N}}\).
Vậy trọng lượng tối đa của các chậu hoa để dây treo không bị đứt là \(37,4{\rm{N}}\).
Đáp án: 37,4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\[\overrightarrow {AC'} = - \overrightarrow a + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b - \overrightarrow c \].
\[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(\left( {3\,;\,4\,;\,0} \right)\).
\(\left( {1\,;\, - 2\,;\, - 2} \right)\).
\(\left( {4\,;\,7\,;\,1} \right)\).
\(\left( {5\,;\,5\,;\, - 1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.