Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu di chuyển với vận tốc và hướng không đổi từ điểm \[M\left( {500;\,200;\,10} \right)\] đến điểm \[N\left( {800;\,300;\,10} \right)\] trong 20 phút.
(a) Máy bay đang di chuyển theo hướng tiến lại gần vị trí đặt ra đa.
(b) Khoảng cách \[MN = 100\sqrt {10} \,{\rm{km}}\].
(c) Tốc độ của máy bay khi di chuyển từ \[M\] đến \[N\] là \[150\sqrt {10} \,{\rm{km/h}}\].
(d) Nếu tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 4 phút tiếp theo là \[Q\left( {a;\,b;\,c} \right)\] với \[a + b + c = 1191\].
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 2 có đáp án !!
Quảng cáo
Trả lời:
a) Sai. Máy bay đang di chuyển từ điểm \[M\left( {500;\,200;\,10} \right)\] đến điểm \[N\left( {800;\,300;\,10} \right)\]. Hoành độ \[x\] và tung \[y\] tăng lên, cao độ \[z\] không đổi. Máy bay đang di chuyển ra xa vị trí đặt ra đa.
b) Đúng. Ta có \[\overrightarrow {MN} \left( {300;\,100;\,0} \right)\] suy ra \(MN = \sqrt {{{300}^2} + {{100}^2} + {0^2}} = 100\sqrt {10} \,\,{\rm{km}}\).
c) Sai. 20 phút \( = \frac{1}{3}\) giờ.
Tốc độ của máy bay khi di chuyển từ \[M\] đến \[N\] là \[\frac{{100\sqrt {10} }}{{\frac{1}{3}}} = 300\sqrt {10} \,\,{\rm{km/h}}\].
d) Sai.

Trong 20 phút, máy bay di chuyển từ điểm \[M\left( {500;\,200;\,10} \right)\] đến điểm \[N\left( {800;\,300;\,10} \right)\].
Nếu giữ nguyên vận tốc và hướng bay thì sau 4 phút tiếp theo máy bay di chuyển đến vị trí điểm \(Q\left( {a;\,b;\,c} \right)\) sao cho \(\overrightarrow {NQ} = \frac{1}{5}\overrightarrow {MN} \).
Suy ra \(\left\{ \begin{array}{l}a - 800 = \frac{1}{5}.300\\b - 300 = \frac{1}{5}.100\\c - 10 = \frac{1}{5}.0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 860\\b = 320\\c = 10\end{array} \right. \Rightarrow Q\left( {860;\,320;\,10} \right)\). Vậy \[a + b + c = 1190\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
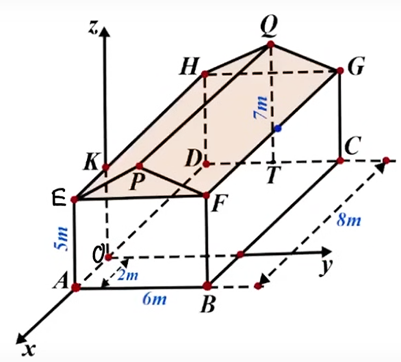
a) Đúng. Tọa độ điểm \(A\) là \(\left( {2;0;0} \right)\).
b) Sai. Ta có \[OD = AD - OA = 8 - 2 = 6\]m.
Tọa độ điểm \[C\left( { - 6;\,6;0} \right)\].
Vì vậy \[\overrightarrow {AC} = \left( { - 8;6;0} \right)\].
c) Sai.Gọi \[M\] là trung điểm của \[HG\] nên \[QM = 7 - 5 = 2\]m, \[MG = \frac{{HG}}{2} = \frac{{AB}}{2} = 3\]m.
Ta có \[QG = \sqrt {Q{M^2} + M{G^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \]m.
Diện tích cần lợp là \[S = 2{S_{PQGF}} = 2.8.\sqrt {13} = 16\sqrt {13} \]m.
Số tiền cần phải trả là \[S.22.11\,000 \approx 13\,961\,000\] đồng.
d) Đúng. Gọi \[J\] là trung điểm của \[BC\] nên \[J\left( { - 2;6;0} \right)\].
Suy ra \[I\] là trung điểm của \[FG\] nên \[I\left( { - 2;6;5} \right)\].
Ta có \[KI = \sqrt {{{\left( { - 2} \right)}^2} + {6^2} + {0^2}} = 2\sqrt {10} \]m.
Vì vậy \[{d_{\min }} = OK + KI = 5 + 2\sqrt {10} \].
Lời giải
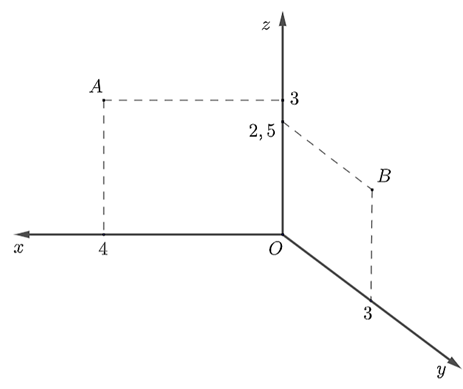
Vì \[M\] thuộc mặt phẳng sàn nhà có chiều dài 8 m, rộng 6 m nên \[M\left( {x;y;0} \right)\] với \[0 \le x \le 8,0 \le y \le 6\].
Cây quạt \[A\] treo chính giữa bức tường 8 m và cách trần 1 m, cây quạt \[B\] treo chính giữa bức tường 6 m và cách trần 1,5 m.
Suy ra \[A\left( {4;0;3} \right),B\left( {0,3,\frac{5}{2}} \right)\].
Ta có: \[\overrightarrow {MA} = \left( {4 - x, - y,3} \right),\overrightarrow {MB} = \left( { - x,3 - y,\frac{5}{2}} \right)\], \[\left| {\overrightarrow {MA} - 2\overrightarrow {MB} } \right| = \sqrt {{{\left( {x + 4} \right)}^2} + {{\left( {y - 6} \right)}^2} + 4} \].
Để \[\left| {\overrightarrow {MA} - 2\overrightarrow {MB} } \right|\] nhỏ nhất thì \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2}\] nhỏ nhất.
Ta có: \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2} \ge {\left( {0 + 4} \right)^2} + 0 = 16\].
Dấu bằng xảy ra khi \[x = 0,y = 6\].
Vậy \[{x^2} + {y^2} + {z^2} = {0^2} + {6^2} + {0^2} = 36\].
Đáp án: 36.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
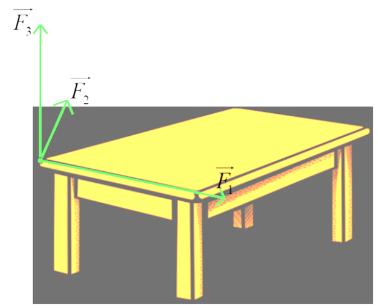
Câu 6
\(\alpha = 180^\circ \).
\(\alpha = 0^\circ \).
\(\alpha = 90^\circ \).
\(\alpha = 45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.