Đề kiểm tra Toán 12 Cánh diều Chương 2 có đáp án - Đề 2
28 người thi tuần này 4.6 262 lượt thi 11 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
Lời giải
Đáp án đúng: B
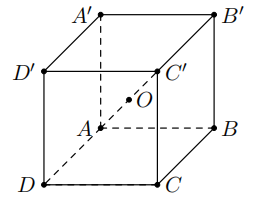
Ta có \[\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \].
Mặt khác \[O\] là trung điểm \[AC' \Rightarrow \overrightarrow {AO} = \frac{1}{2}\overrightarrow {AC'} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
Câu 2
\(\alpha = 180^\circ \).
\(\alpha = 0^\circ \).
\(\alpha = 90^\circ \).
\(\alpha = 45^\circ \).
Lời giải
Đáp án đúng: A
Mà theo giả thiết \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\), suy ra \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 1 \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 180^\circ \).
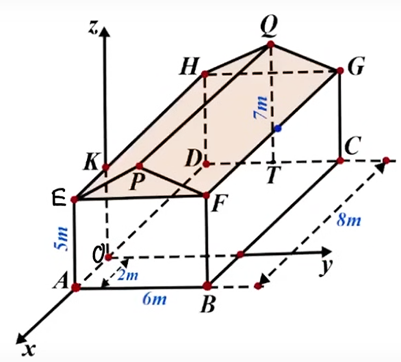
Câu 3
\[90^\circ \].
\[60^\circ \].
\[45^\circ \].
\[120^\circ \].
Lời giải
Đáp án đúng: C
Ta có: \(EG{\rm{//}}AC\) (do \(ACGE\) là hình chữ nhật)\[ \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = 45^\circ \].
Câu 4
\(\left( { - 2\,;\, - 1\,;\, - 3} \right)\).
\(\left( { - 3\,;\,2\,;\, - 1} \right)\).
\(\left( {2\,;\, - 3\,;\, - 1} \right)\).
\(\left( { - 1\,;\,2\,;\, - 3} \right)\).
Lời giải
Đáp án đúng: D
Ta có \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \) nên\(\overrightarrow a = \left( { - 1\,;\,2\,;\, - 3} \right)\).
Câu 5
\(\left( {6; - 2;4} \right)\).
\(\left( {3; - 1;2} \right)\).
\(\left( {1; - 2; - 1} \right)\).
\(\left( {2; - 4; - 2} \right)\).
Lời giải
Đáp án đúng: B
Ta có tọa độ trung điểm \(I\left( {{x_I};{y_I};{z_I}} \right)\) là \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{2 + 4}}{2} = 3\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{1 + \left( { - 3} \right)}}{2} = - 1\\{z_I} = \frac{{{z_A} + {z_B}}}{2} = \frac{{3 + 1}}{2} = 2\end{array} \right.\)\( \Rightarrow I\left( {3; - 1;2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.