Cho hình lập phương \[ABCD.EFGH\]. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
\[90^\circ \].
\[60^\circ \].
\[45^\circ \].
\[120^\circ \].
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 2 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng: C
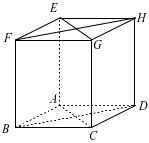
Ta có: \(EG{\rm{//}}AC\) (do \(ACGE\) là hình chữ nhật)\[ \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = 45^\circ \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
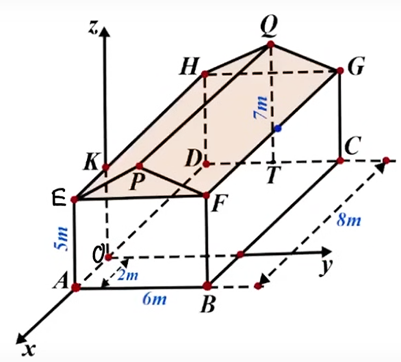
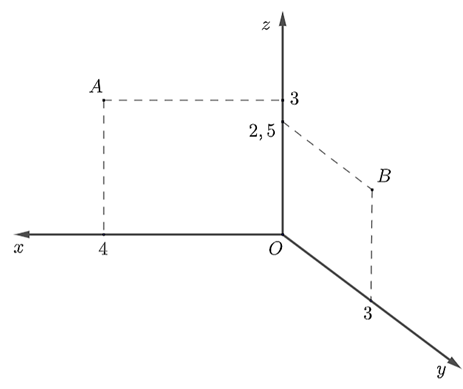
a) Đúng. Tọa độ điểm \(A\) là \(\left( {2;0;0} \right)\).
b) Sai. Ta có \[OD = AD - OA = 8 - 2 = 6\]m.
Tọa độ điểm \[C\left( { - 6;\,6;0} \right)\].
Vì vậy \[\overrightarrow {AC} = \left( { - 8;6;0} \right)\].
c) Sai.Gọi \[M\] là trung điểm của \[HG\] nên \[QM = 7 - 5 = 2\]m, \[MG = \frac{{HG}}{2} = \frac{{AB}}{2} = 3\]m.
Ta có \[QG = \sqrt {Q{M^2} + M{G^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \]m.
Diện tích cần lợp là \[S = 2{S_{PQGF}} = 2.8.\sqrt {13} = 16\sqrt {13} \]m.
Số tiền cần phải trả là \[S.22.11\,000 \approx 13\,961\,000\] đồng.
d) Đúng. Gọi \[J\] là trung điểm của \[BC\] nên \[J\left( { - 2;6;0} \right)\].
Suy ra \[I\] là trung điểm của \[FG\] nên \[I\left( { - 2;6;5} \right)\].
Ta có \[KI = \sqrt {{{\left( { - 2} \right)}^2} + {6^2} + {0^2}} = 2\sqrt {10} \]m.
Vì vậy \[{d_{\min }} = OK + KI = 5 + 2\sqrt {10} \].
Lời giải
Vì \[M\] thuộc mặt phẳng sàn nhà có chiều dài 8 m, rộng 6 m nên \[M\left( {x;y;0} \right)\] với \[0 \le x \le 8,0 \le y \le 6\].
Cây quạt \[A\] treo chính giữa bức tường 8 m và cách trần 1 m, cây quạt \[B\] treo chính giữa bức tường 6 m và cách trần 1,5 m.
Suy ra \[A\left( {4;0;3} \right),B\left( {0,3,\frac{5}{2}} \right)\].
Ta có: \[\overrightarrow {MA} = \left( {4 - x, - y,3} \right),\overrightarrow {MB} = \left( { - x,3 - y,\frac{5}{2}} \right)\], \[\left| {\overrightarrow {MA} - 2\overrightarrow {MB} } \right| = \sqrt {{{\left( {x + 4} \right)}^2} + {{\left( {y - 6} \right)}^2} + 4} \].
Để \[\left| {\overrightarrow {MA} - 2\overrightarrow {MB} } \right|\] nhỏ nhất thì \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2}\] nhỏ nhất.
Ta có: \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2} \ge {\left( {0 + 4} \right)^2} + 0 = 16\].
Dấu bằng xảy ra khi \[x = 0,y = 6\].
Vậy \[{x^2} + {y^2} + {z^2} = {0^2} + {6^2} + {0^2} = 36\].
Đáp án: 36.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(\alpha = 180^\circ \).
\(\alpha = 0^\circ \).
\(\alpha = 90^\circ \).
\(\alpha = 45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.