PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu tương ứng gọi là huyết áp tâm thu và huyết áp tâm trương. Chỉ số huyết áp của chúng ta được viết là tâm thu/tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử một người nào đó có nhịp tim là 70 lần trên phút và huyết áp của người đó được mô hình hóa bởi hàm số \(P\left( t \right) = 100 + 20\sin \left( {\frac{{7\pi }}{3}t} \right)\), trong đó \(P\left( t \right)\) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian \(t\) tính theo giây. Trong khoảng thời gian từ 0 đến 10 giây, hãy xác định số lần huyết áp là 90 mmHg.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu tương ứng gọi là huyết áp tâm thu và huyết áp tâm trương. Chỉ số huyết áp của chúng ta được viết là tâm thu/tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử một người nào đó có nhịp tim là 70 lần trên phút và huyết áp của người đó được mô hình hóa bởi hàm số \(P\left( t \right) = 100 + 20\sin \left( {\frac{{7\pi }}{3}t} \right)\), trong đó \(P\left( t \right)\) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian \(t\) tính theo giây. Trong khoảng thời gian từ 0 đến 10 giây, hãy xác định số lần huyết áp là 90 mmHg.
Quảng cáo
Trả lời:
Trả lời: 23
Ta có \(P\left( t \right) = 90\)\( \Leftrightarrow 100 + 20\sin \left( {\frac{{7\pi }}{3}t} \right) = 90\)\( \Leftrightarrow \sin \left( {\frac{{7\pi }}{3}t} \right) = - \frac{1}{2}\)
\( \Leftrightarrow \sin \left( {\frac{{7\pi }}{3}t} \right) = \sin \left( { - \frac{\pi }{6}} \right)\)\( \Leftrightarrow \left[ \begin{array}{l}t = - \frac{1}{{14}} + \frac{{12}}{{14}}k\\t = \frac{7}{{14}} + \frac{{12}}{{14}}n\end{array} \right.,\left( {k,n \in \mathbb{Z}} \right)\).
Với \(t = - \frac{1}{{14}} + \frac{{12}}{{14}}k\) ta có:
\(0 < - \frac{1}{{14}} + \frac{{12}}{{14}}k < 10\)\( \Leftrightarrow \frac{1}{{12}} < k < \frac{{47}}{4}\)\( \Rightarrow k \in \left\{ {1;2;3;4;5;6;7;8;9;10;11} \right\}\).
Với \(t = \frac{7}{{14}} + \frac{{12}}{{14}}n\) ta có
\(0 < \frac{7}{{14}} + \frac{{12}}{{14}}n < 10\)\( \Leftrightarrow - \frac{7}{{12}} < n < \frac{{133}}{{12}}\)\( \Rightarrow n \in \left\{ {0;1;2;3;4;5;6;7;8;9;10;11} \right\}\).
Vậy trong khoảng thời gian từ 0 đến 10 giây, có 23 lần huyết áp là 90 mmHg.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: C
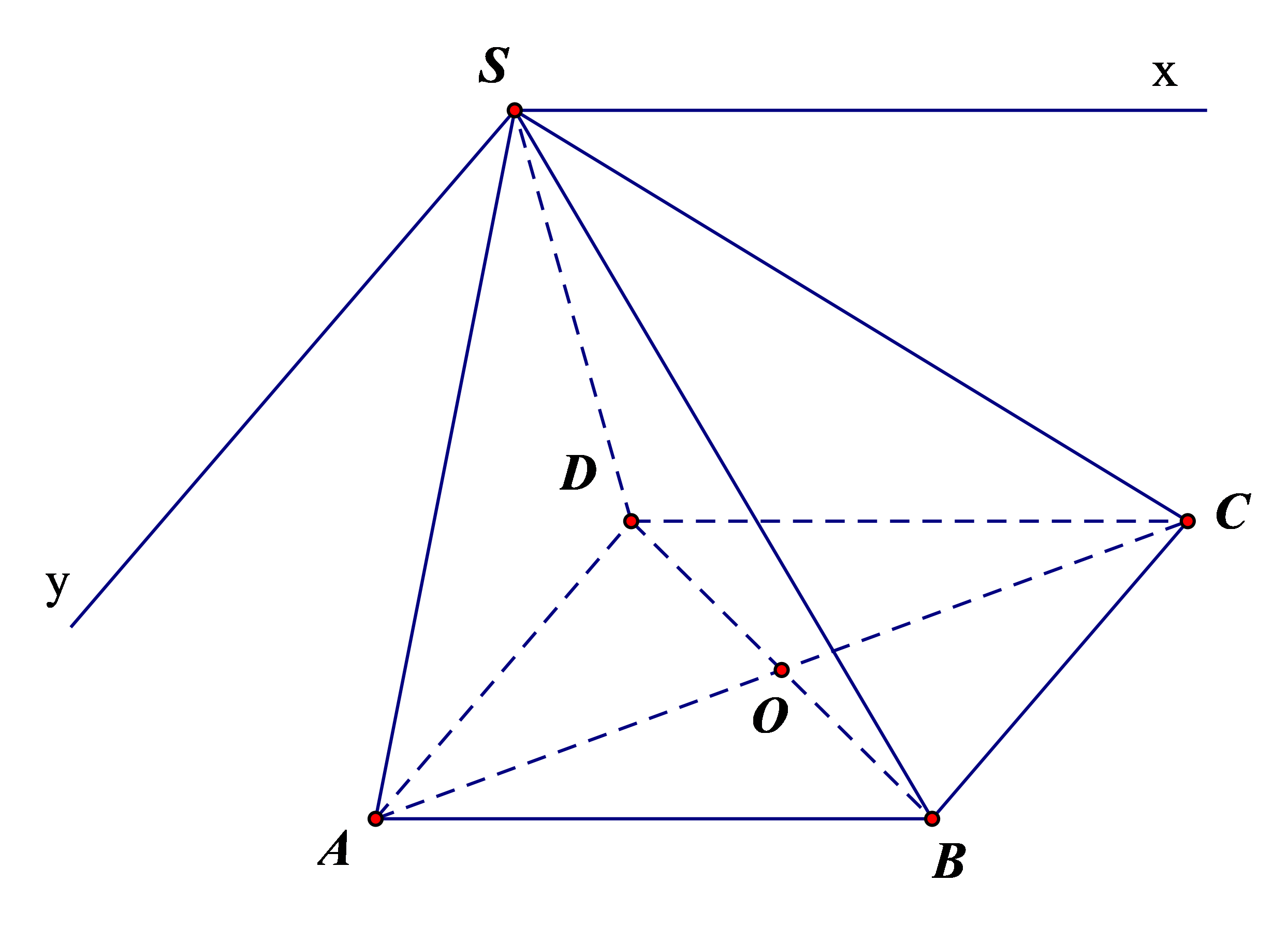
+) Vì \(\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SBD} \right)\end{array} \right.\) nên \(O \in \left( {SAC} \right) \cap \left( {SBD} \right)\).
Lại có \(S \in \left( {SAC} \right) \cap \left( {SBD} \right)\) nên \(SO = \left( {SAC} \right) \cap \left( {SBD} \right)\).
+) Do \(ABCD\) là hình bình hành nên \(AB//CD\) và \(AD//BC\).
Vì \(\left\{ \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\AB//CD//Sx\end{array} \right.\) nên \(Sx = \left( {SAB} \right) \cap \left( {SCD} \right)\).
Vì \(\left\{ \begin{array}{l}S \in \left( {SAD} \right) \cap \left( {SBC} \right)\\AD//BC//Sy\end{array} \right.\) nên \(Sy = \left( {SAD} \right) \cap \left( {SBC} \right)\).
Lời giải
a) Đ, b) S, c) Đ, d) S
a) Ta có \(2\cos \left( {x + \frac{\pi }{4}} \right) - \sqrt 3 = 0 \Leftrightarrow \cos \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \cos \left( {x + \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{6}} \right)\).
b) Ta có \(2\cos \left( {x + \frac{\pi }{4}} \right) - \sqrt 3 = 0 \Leftrightarrow \cos \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \cos \left( {x + \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{6}} \right)\)
\( \Leftrightarrow x + \frac{\pi }{4} = \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}\) hoặc \(x + \frac{\pi }{4} = - \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}\)
\( \Leftrightarrow x = - \frac{\pi }{{12}} + k2\pi ,k \in \mathbb{Z}\) hoặc \[x = - \frac{{5\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\].
c)
- Với \(x = - \frac{\pi }{{12}} + k2\pi ,k \in \mathbb{Z}\)
Vì \(x \in \left( { - \pi ;\pi } \right)\) nên \( - \pi < - \frac{\pi }{{12}} + k2\pi < \pi \Leftrightarrow - \frac{{11\pi }}{{12}} < k2\pi < \frac{{13\pi }}{{12}} \Leftrightarrow - \frac{{11}}{{24}} < k < \frac{{13}}{{24}}\)
Do \(k \in \mathbb{Z}\) nên \(k = 0\). Suy ra \({x_1} = - \frac{\pi }{{12}}\)
- Với \[x = - \frac{{5\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\]
Vì \(x \in \left( { - \pi ;\pi } \right)\) nên \( - \pi < - \frac{{5\pi }}{{12}} + k2\pi < \pi \Leftrightarrow - \frac{{7\pi }}{{12}} < k2\pi < \frac{{17\pi }}{{12}} \Leftrightarrow - \frac{7}{{24}} < k < \frac{{17}}{{24}}\)
Do \(k \in \mathbb{Z}\) nên \(k = 0\). Suy ra \({x_2} = - \frac{{5\pi }}{{12}}\).
d) Ta có \(S = {x_1} + {x_2} = - \frac{{5\pi }}{{12}} - \frac{\pi }{{12}} = - \frac{\pi }{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.