Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
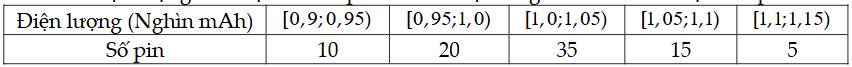
Khi đó:
a) Số trung bình của dãy số liệu là: 1,016.
b) Mốt của dãy số liệu là 1,05.
c) Tứ phân vị thứ nhất của mẫu số liệu nhóm là \({Q_1} \approx 0,98\).
d) Tứ phân vị thứ ba của mẫu số liệu nhóm là \({Q_3} \approx 1,248\).
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
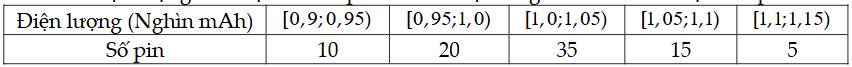
Khi đó:
a) Số trung bình của dãy số liệu là: 1,016.
b) Mốt của dãy số liệu là 1,05.
c) Tứ phân vị thứ nhất của mẫu số liệu nhóm là \({Q_1} \approx 0,98\).
d) Tứ phân vị thứ ba của mẫu số liệu nhóm là \({Q_3} \approx 1,248\).
Quảng cáo
Trả lời:
a) Đ, b) S, c) Đ, d) S
Ta có bảng sau

a) Số trung bình của dãy số liệu là:
\(\frac{{0,925.10 + 0,975.20 + 1,025.35 + 1,075.15 + 1,125.5}}{{85}} \approx 1,016.\)
b) Nhóm chứa mốt của dãy số liệu là \(\left[ {1;1,05} \right)\).
Ta có \({M_0} = 1 + \frac{{35 - 20}}{{\left( {35 - 20} \right) + \left( {35 - 15} \right)}}.\left( {1,05 - 1} \right) \approx 1,02\).
c) Gọi \({x_1};{x_2};...;{x_{85}}\) lần lượt là điện lượng mỗi viên pin xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\) mà \({x_{21}};{x_{22}} \in \left[ {0,95;1} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu là \({Q_1} = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}\left( {1 - 0,95} \right) \approx 0,98\).
d) Tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\) mà \({x_{64}},{x_{65}} \in \left[ {1;1,05} \right)\) nên tứ phân vị thứ ba của mẫu số liệu là \({Q_3} = 1 + \frac{{\frac{{3.85}}{4} - 30}}{{35}}\left( {1,05 - 1} \right) \approx 1,048\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) Đ, c) Đ, d) S
a) Ta có \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \left( {x - 2} \right) = - 4\).
b) Ta có \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {x - 2} \right) = - 3\).
c) Ta có \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \sqrt {{x^2} + 1} = \sqrt 2 \).
d) Vì \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\).
Câu 2
Lời giải
Đáp án đúng là: A
\({u_4} = \frac{4}{{{2^4}}} = \frac{1}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
