Hình bên dưới là kệ sách gỗ có bốn mặt kệ, với thanh gỗ đứng (xem như đường thẳng d1) và thanh gỗ xiên (xem như đường thẳng d2). Giả sử các mặt kệ xuất hiện ở các vị trí \(A,B,C,D,E,F,G,H\). Biết rằng \(EF = 32\) cm và các điểm \(A,B,C,D\) cách đều nhau. Các mặt kệ đặt song song với mặt đất. Tính độ dài HE.
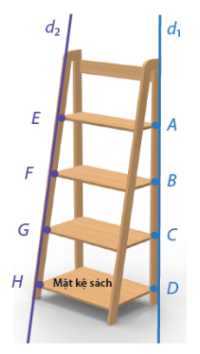
Hình bên dưới là kệ sách gỗ có bốn mặt kệ, với thanh gỗ đứng (xem như đường thẳng d1) và thanh gỗ xiên (xem như đường thẳng d2). Giả sử các mặt kệ xuất hiện ở các vị trí \(A,B,C,D,E,F,G,H\). Biết rằng \(EF = 32\) cm và các điểm \(A,B,C,D\) cách đều nhau. Các mặt kệ đặt song song với mặt đất. Tính độ dài HE.

Quảng cáo
Trả lời:
Các mặt kệ sách đặt song song với mặt đất nên là hình ảnh của các mặt phẳng song song nhau, ta kí hiệu các mặt phẳng từ đáy kệ sách lên trên lần lượt là \(\left( {{P_1}} \right),\left( {{P_2}} \right),\left( {{P_3}} \right),\left( {{P_4}} \right)\).
Áp dụng định lí Thales cho ba mặt phẳng \(\left( {{P_1}} \right),\left( {{P_2}} \right),\left( {{P_3}} \right)\) với hai cát tuyến \({d_1};{d_2}\) ta có \(\frac{{FG}}{{BC}} = \frac{{GH}}{{CD}} \Rightarrow \frac{{FG}}{{GH}} = \frac{{BC}}{{CD}}\).
Mà \(BC = CD\) nên \(\frac{{FG}}{{GH}} = 1 \Rightarrow FG = GH\).
Tương tự áp dụng định lí Thales cho ba mặt phẳng \(\left( {{P_2}} \right),\left( {{P_3}} \right),\left( {{P_4}} \right)\) với hai cát tuyến \({d_1};{d_2}\) ta có \(EF = FG\).
Từ đó suy ra \(GH = FG = EF = 32\) cm.
Vậy \(HE = EF + FG + GH = 96\)cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

Gọi \(N\) là trung điểm của \(AB\), M là trung điểm \(AC\).
Suy ra \(MN\)là đường trung bình của \(\Delta ABC\). Do đó \(MN//BC\).
Do đó \(N\)là hình chiếu song song của điểm \(M\) lên \(\left( {AA'B'} \right)\) theo phương chiếu \(CB\).
Do đó \(\frac{{MN}}{{BC}} = \frac{1}{2} = 0,5\).
Trả lời: 0,5.
Lời giải
Gọi \({h_n}\) là độ cao quả bóng đạt được ở lần nảy thứ \(n\).
Theo bài ra ta có \({h_n} = \frac{3}{{10}}{h_{n - 1}}\) nên \(\left( {{h_n}} \right)\) là 1 cấp số nhân với \({h_1} = \frac{3}{{10}}.7,2\) với công bội \(q = \frac{3}{{10}}\) (là cấp số nhân lùi vô hạn).
Gọi \({v_n}\) là độ dài quãng đường bóng rơi từ trên xuống đất lần thứ \(n\).
Theo bài ta ta có \({v_n} = \frac{3}{{10}}{v_{n - 1}}\) nên \(\left( {{v_n}} \right)\) là một cấp số nhân với \({v_1} = 7,2\) và công bội \(q = \frac{3}{{10}}\) (là cấp số nhân lùi vô hạn).
Nếu quá trình bóng rơi xuống, nảy lên diễn ra mãi thì tổng quãng đường bóng di chuyển được bằng:
\(\mathop {\lim }\limits_{n \to + \infty } {S_n} = \mathop {\lim }\limits_{n \to + \infty } \left[ {\left( {{v_1} + {v_2} + ... + {v_n} + ...} \right) + \left( {\left( {{h_1} + {h_2} + ... + {h_n} + ...} \right)} \right)} \right]\)
\( = \left( {7,2.\frac{1}{{1 - \frac{3}{{10}}}}} \right) + \left( {7,2.\frac{3}{{10}}.\frac{1}{{1 - \frac{3}{{10}}}}} \right) = \frac{{468}}{{35}} \approx 13,4\) (m).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho lăng trụ tứ giác \(ABCD.A'B'C'D'\) có hai đáy \(ABCD\) và \(A'B'C'D'\)là hai hình bình hành.
a) Lăng trụ tứ giác \(ABCD.A'B'C'D'\)là hình hộp.
b) Tứ giác \(ABC'D'\) là hình chữ nhật.
c) Đường thẳng \(AD'\)song song với mặt phẳng \(\left( {BDC'} \right)\).
d) Mặt phẳng \(\left( {ACD'} \right)\)song song với mặt phẳng \(\left( {BA'C'} \right)\).
Cho lăng trụ tứ giác \(ABCD.A'B'C'D'\) có hai đáy \(ABCD\) và \(A'B'C'D'\)là hai hình bình hành.
a) Lăng trụ tứ giác \(ABCD.A'B'C'D'\)là hình hộp.
b) Tứ giác \(ABC'D'\) là hình chữ nhật.
c) Đường thẳng \(AD'\)song song với mặt phẳng \(\left( {BDC'} \right)\).
d) Mặt phẳng \(\left( {ACD'} \right)\)song song với mặt phẳng \(\left( {BA'C'} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

