Thời gian chờ xe buýt (đơn vị: phút) của 13 học sinh tại một bến xe buýt được thống kê như sau:
3
6
4
25
8
10
12
15
6
3
5
7
a) Giá trị lớn nhất của mẫu số liệu là 25.
b) Khoảng biến thiên của mẫu số liệu là 25.
c) Trung vị của mẫu số liệu là 5.
d) Khoảng tứ phân vị của mẫu số liệu là \({\Delta _Q} = 7,5\).
Thời gian chờ xe buýt (đơn vị: phút) của 13 học sinh tại một bến xe buýt được thống kê như sau:
|
3 |
6 |
4 |
25 |
8 |
10 |
12 |
15 |
6 |
3 |
5 |
7 |
a) Giá trị lớn nhất của mẫu số liệu là 25.
b) Khoảng biến thiên của mẫu số liệu là 25.
c) Trung vị của mẫu số liệu là 5.
d) Khoảng tứ phân vị của mẫu số liệu là \({\Delta _Q} = 7,5\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Sắp xếp mẫu số liệu theo thứ tự không giảm ta được
|
1 |
3 |
|
3 |
4 |
5 |
6 |
6 |
7 |
8 |
10 |
12 |
15 |
25 |
a) Giá trị lớn nhất của mẫu số liệu là 25.
b) Khoảng biến thiên của mẫu số liệu là R = 25 – 1 = 24.
c) Vì kích thước của mẫu số liệu là 13 nên Q2 là giá trị chính giữa của mẫu nên \({Q_2} = 6\) \( \Rightarrow {M_e} = 6\).
d) Nửa số liệu bên phải \({Q_2}\) là
|
7 |
8 |
10 |
12 |
15 |
25 |
Tứ phân vị thứ ba của mẫu số liệu là \({Q_3} = \frac{{10 + 12}}{2} = 11\).
Nửa số liệu bên trái Q2 là
|
1 |
3 |
3 |
4 |
5 |
6 |
Tứ phân vị thứ nhất của mẫu số liệu là \({Q_1} = \frac{{3 + 4}}{2} = 3,5\).
Khoảng tứ phân vị của mẫu số liệu là \({\Delta _Q} = {Q_3} - {Q_1} = 11 - 3,5 = 7,5\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
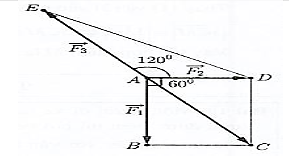
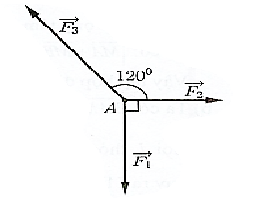
Đặt \(\overrightarrow {{F_1}} = \overrightarrow {AB} ,\overrightarrow {{F_2}} = \overrightarrow {AD} ,\overrightarrow {{F_3}} = \overrightarrow {AE} \).
Vẽ hình chữ nhật ABCD.
Vì vật ở trạng thái cân bằng nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \) \( \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AE} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {AC} = - \overrightarrow {AE} \).
Ta có \(AB = 12,\widehat {CAD} = 180^\circ - 120^\circ = 60^\circ \Rightarrow \widehat {BAC} = 30^\circ \).
Tam giác ABC vuông tại B nên \(BC = AB\tan 30^\circ = 12.\frac{{\sqrt 3 }}{3} = 4\sqrt 3 = AD\).
Độ lớn lực \(\overrightarrow {{F_2}} \) bằng \(4\sqrt 3 \) N.
Ta có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{12}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 8\sqrt 3 \).
Do vậy \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {AE} } \right| = AC = 8\sqrt 3 \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
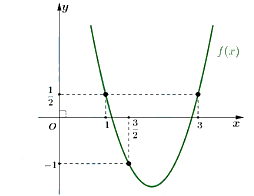
a) Dựa vào đồ thị ta thấy \(f\left( 1 \right) = \frac{1}{2}\).
b) Bề lõm của đồ thị quay lên trên nên \(a > 0\).
c) Có \(a + b + c = f\left( 1 \right) = \frac{1}{2} < 1\).
d) Từ đồ thị ta có hệ phương trình \(\left\{ \begin{array}{l}f\left( 1 \right) = \frac{1}{2}\\f\left( {\frac{3}{2}} \right) = - 1\\f\left( 3 \right) = \frac{1}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a + b + c = \frac{1}{2}\\\frac{9}{4}a + \frac{3}{2}b + c = - 1\\9a + 3b + c = \frac{1}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 8\\c = \frac{{13}}{2}\end{array} \right.\).
Suy ra \(a - b = 10\).
Đáp án: a) Sai; b) Đúng; c) Sai; d) Đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x = 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập