Gọi \({x_1}\) là nghiệm của phương trình \(\sqrt {2x - 1}  = \sqrt 3 \).        \(\left( 1 \right)\)

\({x_2}\) là nghiệm của phương trình \(\sqrt[3]{{ - 3x + 1}} = \sqrt[3]{2}\).           \(\left( 2 \right)\)

a) Phương trình \(\left( 1 \right)\) có một nghiệm \({x_1} = 5\).

b) Phương trình \(\left( 2 \right)\) có một nghiệm \({x_2} = \frac{{ - 1}}{3}\).

c) \({x_1} + {x_2} = \frac{5}{3}\).

d) \({x_1}{x_2} = \frac{2}{3}\).

Quãng đường anh An đi từ nhà tới trường là: \(4 \cdot \frac{{15}}{{60}} = 1\,\,\left( {{\rm{km}}} \right)\).

Quãng đường em Bình từ nhà đến trường là \(3 \cdot \frac{{12}}{{60}} = 0,6\,\,\left( {{\rm{km}}} \right)\).

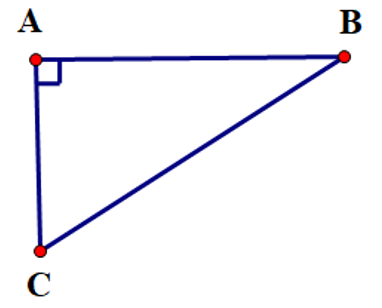
Áp dụng định lí Pythagore vào tam giác \(ABC\) vuông tại \(A\), ta có:

\(B{C^2} = A{B^2} + A{C^2} = {1^2} + {\left( {0,6} \right)^2} = 1,36\) hay \(BC = \sqrt {1,36}  \approx 1,17\,\,\left( {{\rm{km}}} \right)\).

Vậy khoảng cách \(BC\) giữa hai trường khoảng \(1,17\,\,{\rm{km}}\).

Đáp án: 1,17.

a) Đúng. Ta có \[A = \sqrt {25{x^2}}  - 7x = 5\left| x \right| - 7x.\]

b) Sai. Vì \[x \ge 0\] nên \[A = 5\left| x \right| - 7x = 5x - 7x =  - 2x.\]  

c) Đúng. Thay \[x =  - 3\] vào biểu thức \[A = 5\left| x \right| - 7x = 5 \cdot 3 - 7 \cdot \left( { - 3} \right) = 36.\]

d) Sai. Với \[x < 0\] nên \[A =  - 5x - 7x =  - 12x\]. Để \[A = 24\] thì \[ - 12x = 24\] nên \[x =  - 2\].