Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai

Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Một chiếc xe khách đi từ Thành phố Hồ Chí Minh đến Cần Thơ, quãng đường dài \(170\) km. Sau khi xe khách xuất phát 1 giờ 40 phút, một xe tải bắt đầu đi từ Cần Thơ về Thành phố Hồ Chí Minh và gặp xe khách sau đó 40 phút. Biết rằng mỗi giờ xe khách đi nhanh hơn xe tải là \(15\) km. Gọi \(x\) là vận tốc của xe tải, \(y\) là vận tốc của xe khách (\(y > x > 0\), km/h).

    a) \(y - x = 15.\)

    b) Phương trình biểu diễn quãng đường Thành phố Hồ Chí Minh – Cần Thơ là \(\frac{7}{3}x + \frac{2}{3}y = 170.\)

    c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}y - x = 15\\\frac{7}{3}x + \frac{2}{3}y = 170\end{array} \right.\).

    d) Vận tốc của xe tải là \(60\)km/h, vận tốc của xe khách là 45 km/h.

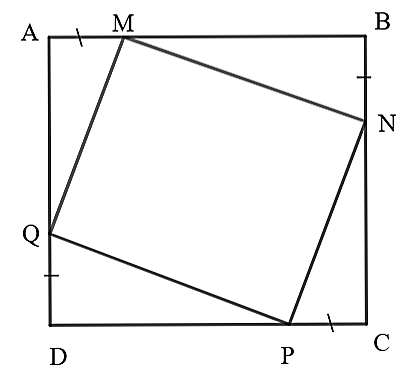
Coi các sân đó là hình vuông \[ABCD\], phần lát gạch đỏ trang trí là hình vuông \[MNPQ\].

Ta chứng minh được \[\Delta AMQ = \Delta BNM = \Delta CPN = \Delta DQP\] (c.c.c)

Diện tích hình vuông \[MNPQ\] có diện tích nhỏ nhất khi tổng diện tích bốn tam giác vuông ở bốn góc hình vuông \[ABCD\] là lớn nhất.

Gọi \[S = {S_{AMQ}} + {S_{BNM}} + {S_{CPN}} + {S_{DQP}} = 4{S_{AMQ}} = 4 \cdot \frac{1}{2}AM \cdot AQ = 2 \cdot AM \cdot AQ\]

Mà \[AM + AQ = AM + MB = 16\,\,\left( {\rm{m}} \right)\].

Lại có \[{\left( {AM - MB} \right)^2} \ge 0\]

Suy ra \[A{M^2} + M{B^2} \ge 2MA \cdot MB\]

Do đó, \[A{M^2} + 2MA \cdot MB + M{B^2} \ge 4MA \cdot MB\]

             \[{\left( {MA + MB} \right)^2} \ge 4MA \cdot MB\]

Suy ra \[2MA \cdot MB \le \frac{{{{\left( {MA + MB} \right)}^2}}}{2} = \frac{{{{16}^2}}}{2} = 128\] hay \[S \le 128\].

Dấu “=” xảy ra khi \[MA = MB = \frac{{AB}}{2} = 8{\rm{ }}\left( {\rm{m}} \right)\].

Khi đó, \[M,\,N,\,P,\,Q\] lần lượt là trung điểm của các cạnh \[AB,\,BC,\,CD,\,DA.\]

Vậy khi \[M,\,N,\,P,\,Q\] lần lượt là trung điểm của các cạnh \[AB,\,BC,\,CD,\,DA\] thì diện tích hình vuông \[MNPQ\] nhỏ nhất.

Hướng dẫn giải

a) Với \(a \ge 0,{\rm{ }}a \ne 16\), ta có:

\(C = \frac{a}{{a - 16}} - \frac{2}{{\sqrt a - 4}} - \frac{2}{{\sqrt a + 4}}\)

   \[ = \frac{a}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}} - \frac{{2\left( {\sqrt a + 4} \right)}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}} - \frac{{2\left( {\sqrt a - 4} \right)}}{{\left( {\sqrt a + 4} \right)\left( {\sqrt a - 4} \right)}}\]

\[ = \frac{{a - 2\sqrt a - 8 - 2\sqrt a + 8}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{a - 4\sqrt a }}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{\sqrt a \left( {\sqrt a - 4} \right)}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{\sqrt a }}{{\sqrt a + 4}}.\]

Vậy với \(a \ge 0,{\rm{ }}a \ne 16\) có \[C = \frac{{\sqrt a }}{{\sqrt a + 4}}.\]

b) Ta có: \(a = 9 - 4\sqrt 5 = 5 - 2 \cdot 2 \cdot \sqrt 5 + 4 = {\left( {\sqrt 5 - 2} \right)^2}\).

Thay vào \[C,\] ta được:

\[C = \frac{{\sqrt a }}{{\sqrt a + 4}} = \frac{{\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} }}{{\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} + 4}} = \frac{{\sqrt 5 - 2}}{{\sqrt 5 + 2}} = \frac{{{{\left( {\sqrt 5 - 2} \right)}^2}}}{{\left( {\sqrt 5 + 2} \right)\left( {\sqrt 5 - 2} \right)}} = \frac{{9 - 4\sqrt 5 }}{{5 - 4}} = 9 - 4\sqrt 5 \].

Vậy giá trị của \(C = 9 - 4\sqrt 5 \) tại \(a = 9 - 4\sqrt 5 .\)