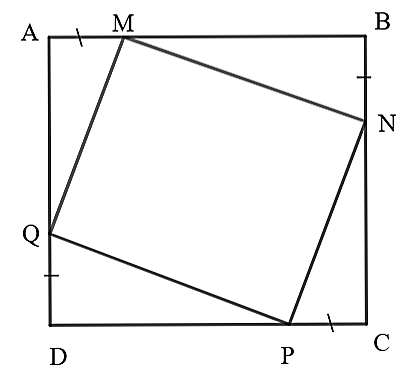
(0,5 điểm) Nhà bác Hương có một mảnh sân hình vuông có cạnh là \[16{\rm{ m}}{\rm{.}}\] Bác Hương muốn lát gạch màu đỏ có dạng hình vuông \[MNPQ\] để trang trí lên mảnh sân hình vuông (như hình vẽ). Tìm vị trí của các điểm \[M,\,N,\,P,\,Q\] lần lượt trên các cạnh của mảnh sân để hình vuông \[MNPQ\] có diện tích nhỏ nhất.

Hướng dẫn giải

a) Với \(a \ge 0,{\rm{ }}a \ne 16\), ta có:

\(C = \frac{a}{{a - 16}} - \frac{2}{{\sqrt a - 4}} - \frac{2}{{\sqrt a + 4}}\)

   \[ = \frac{a}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}} - \frac{{2\left( {\sqrt a + 4} \right)}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}} - \frac{{2\left( {\sqrt a - 4} \right)}}{{\left( {\sqrt a + 4} \right)\left( {\sqrt a - 4} \right)}}\]

\[ = \frac{{a - 2\sqrt a - 8 - 2\sqrt a + 8}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{a - 4\sqrt a }}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{\sqrt a \left( {\sqrt a - 4} \right)}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{\sqrt a }}{{\sqrt a + 4}}.\]

Vậy với \(a \ge 0,{\rm{ }}a \ne 16\) có \[C = \frac{{\sqrt a }}{{\sqrt a + 4}}.\]

b) Ta có: \(a = 9 - 4\sqrt 5 = 5 - 2 \cdot 2 \cdot \sqrt 5 + 4 = {\left( {\sqrt 5 - 2} \right)^2}\).

Thay vào \[C,\] ta được:

\[C = \frac{{\sqrt a }}{{\sqrt a + 4}} = \frac{{\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} }}{{\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} + 4}} = \frac{{\sqrt 5 - 2}}{{\sqrt 5 + 2}} = \frac{{{{\left( {\sqrt 5 - 2} \right)}^2}}}{{\left( {\sqrt 5 + 2} \right)\left( {\sqrt 5 - 2} \right)}} = \frac{{9 - 4\sqrt 5 }}{{5 - 4}} = 9 - 4\sqrt 5 \].

Vậy giá trị của \(C = 9 - 4\sqrt 5 \) tại \(a = 9 - 4\sqrt 5 .\)

Hướng dẫn giải

Đáp án đúng là: a) Sai.         b) Sai.              c) Đúng.        d) Đúng.

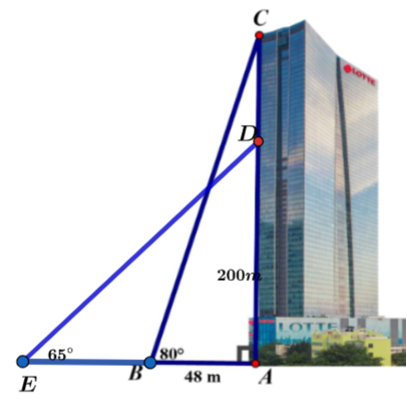
• Từ hình vẽ, ta xét tam giác vuông \(ABC\), có:

\(AC = AB.\tan \widehat {CBA} = 48.\tan 80^\circ \approx 272,22{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)

Do đó, ý a) là sai.

• Do người đó có tầm mắt \[1,65{\rm{ m}}\] nên chiều cao của tòa nhà là:

\[272,22 - 1,65 = 270,57{\rm{ }}\left( {\rm{m}} \right)\].

Vậy tòa nhà cao \[270,57{\rm{ m}}\].

Do đó, ý b) là sai.

• Khoảng cách từ xe thu gom phế thải ở \[E\] đến chân tòa nhà là độ dài đoạn \[EA\].

Xét tam giác vuông \[EAD\], ta có:

\[EA = \frac{{AD}}{{\tan \widehat {DEA}}} = \frac{{200}}{{\tan 65^\circ }} \approx 93,26{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]

Do đó, ý c) là đúng.

• Khoảng cách của hai xe thu gom phế thải là \[93,26 - 48 = 45,26{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]

Vậy hai xe thu gom phế thải cách nhau \[45,26{\rm{ m}}\].

Vậy ý d) là đúng.