Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn

Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Tìm giá trị của \[x\] thỏa mãn phương trình \(\frac{x}{{2x - 6}} + \frac{x}{{2x + 2}} = \frac{{ - 2x}}{{\left( {3 - x} \right)\left( {x + 1} \right)}}\).

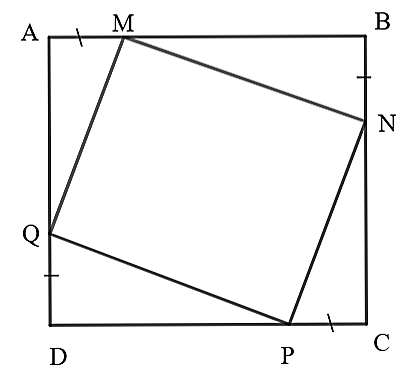
Coi các sân đó là hình vuông \[ABCD\], phần lát gạch đỏ trang trí là hình vuông \[MNPQ\].

Ta chứng minh được \[\Delta AMQ = \Delta BNM = \Delta CPN = \Delta DQP\] (c.c.c)

Diện tích hình vuông \[MNPQ\] có diện tích nhỏ nhất khi tổng diện tích bốn tam giác vuông ở bốn góc hình vuông \[ABCD\] là lớn nhất.

Gọi \[S = {S_{AMQ}} + {S_{BNM}} + {S_{CPN}} + {S_{DQP}} = 4{S_{AMQ}} = 4 \cdot \frac{1}{2}AM \cdot AQ = 2 \cdot AM \cdot AQ\]

Mà \[AM + AQ = AM + MB = 16\,\,\left( {\rm{m}} \right)\].

Lại có \[{\left( {AM - MB} \right)^2} \ge 0\]

Suy ra \[A{M^2} + M{B^2} \ge 2MA \cdot MB\]

Do đó, \[A{M^2} + 2MA \cdot MB + M{B^2} \ge 4MA \cdot MB\]

             \[{\left( {MA + MB} \right)^2} \ge 4MA \cdot MB\]

Suy ra \[2MA \cdot MB \le \frac{{{{\left( {MA + MB} \right)}^2}}}{2} = \frac{{{{16}^2}}}{2} = 128\] hay \[S \le 128\].

Dấu “=” xảy ra khi \[MA = MB = \frac{{AB}}{2} = 8{\rm{ }}\left( {\rm{m}} \right)\].

Khi đó, \[M,\,N,\,P,\,Q\] lần lượt là trung điểm của các cạnh \[AB,\,BC,\,CD,\,DA.\]

Vậy khi \[M,\,N,\,P,\,Q\] lần lượt là trung điểm của các cạnh \[AB,\,BC,\,CD,\,DA\] thì diện tích hình vuông \[MNPQ\] nhỏ nhất.

Hướng dẫn giải

a) Với \(a \ge 0,{\rm{ }}a \ne 16\), ta có:

\(C = \frac{a}{{a - 16}} - \frac{2}{{\sqrt a - 4}} - \frac{2}{{\sqrt a + 4}}\)

   \[ = \frac{a}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}} - \frac{{2\left( {\sqrt a + 4} \right)}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}} - \frac{{2\left( {\sqrt a - 4} \right)}}{{\left( {\sqrt a + 4} \right)\left( {\sqrt a - 4} \right)}}\]

\[ = \frac{{a - 2\sqrt a - 8 - 2\sqrt a + 8}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{a - 4\sqrt a }}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{\sqrt a \left( {\sqrt a - 4} \right)}}{{\left( {\sqrt a - 4} \right)\left( {\sqrt a + 4} \right)}}\]

\[ = \frac{{\sqrt a }}{{\sqrt a + 4}}.\]

Vậy với \(a \ge 0,{\rm{ }}a \ne 16\) có \[C = \frac{{\sqrt a }}{{\sqrt a + 4}}.\]

b) Ta có: \(a = 9 - 4\sqrt 5 = 5 - 2 \cdot 2 \cdot \sqrt 5 + 4 = {\left( {\sqrt 5 - 2} \right)^2}\).

Thay vào \[C,\] ta được:

\[C = \frac{{\sqrt a }}{{\sqrt a + 4}} = \frac{{\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} }}{{\sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} + 4}} = \frac{{\sqrt 5 - 2}}{{\sqrt 5 + 2}} = \frac{{{{\left( {\sqrt 5 - 2} \right)}^2}}}{{\left( {\sqrt 5 + 2} \right)\left( {\sqrt 5 - 2} \right)}} = \frac{{9 - 4\sqrt 5 }}{{5 - 4}} = 9 - 4\sqrt 5 \].

Vậy giá trị của \(C = 9 - 4\sqrt 5 \) tại \(a = 9 - 4\sqrt 5 .\)