Bạn An đi xe đạp từ \[A\] đến địa điểm \[B\] phải leo lên một con dốc \[AC\] và xuống một con dốc \[CB\] (như hình vẽ). Cho biết con dốc \[AC\] dài \[440{\rm{ m}}\,{\rm{;}}\] \(\widehat A = 6^\circ ,\,\,\widehat B = 4^\circ \). Biết vận tốc trung bình lúc xuống dốc là \(18\;\,{\rm{km}}/{\rm{h}}\).
Thời gian bạn An đi xe đạp xuống dốc từ \[C\] đến \[B\] là
Thời gian bạn An đi xe đạp xuống dốc từ \[C\] đến \[B\] là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn D
Đổi \(18\;\,{\rm{km}}/{\rm{h}} = 30\;\,{\rm{m}}/{\rm{s}}\).
• Xét \(\Delta AHC\) vuông tại \[H,\] ta có:
\(\sin \widehat {HAC} = \frac{{CH}}{{AC}}\) hay \(\sin 6^\circ = \frac{{CH}}{{440}}\) nên \(CH = 440 \cdot \sin 6^\circ = 46\;\,({\rm{m}})\).
• Xét \(\Delta BHC\) vuông tại H, ta có:
\(\sin \widehat {HBC} = \frac{{CH}}{{BC}}\) hay \(\sin 4^\circ = \frac{{46}}{{BC}}\) nên \(BC = \frac{{46}}{{\sin 4^\circ }} = 659\;\,({\rm{m}})\).
Thời gian bạn An đi xe đạp xuống dốc từ \[C\] đến \[B\] là:
\(\frac{{659}}{{30}}\) phút \( = 21\) phút 58 giây.
Vậy thời gian bạn An đi xe đạp xuống dốc từ \[C\] đến \[B\] là 21 phút 58 giây.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
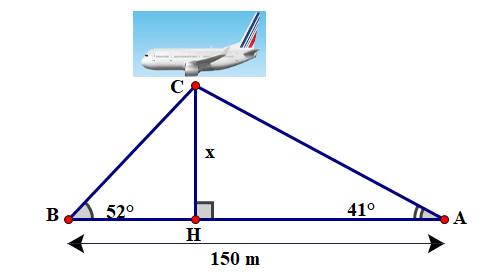
Đặt \(CH = x\,\,(\;{\rm{m}}),\,\,x > 0\).
• Xét \(\Delta HBC\) vuông tại \[H,\] ta có:
\(\tan \widehat {CBH} = \frac{{CH}}{{BH}}\) hay \(\tan 52^\circ = \frac{x}{{BH}}\) nên \(BH = \frac{x}{{\tan 52^\circ }}\).
• Xét \(\Delta HAC\) vuông tại \[H,\] ta có:
\(\tan \widehat {CAH} = \frac{{CH}}{{AH}}\) hay \(\tan 41^\circ = \frac{x}{{AH}}\) nên \(AH = \frac{x}{{\tan 41^\circ }}\).
Ta có: \(HB + HA = AB\)
\(\frac{x}{{\tan 52^\circ }} + \frac{x}{{\tan 41^\circ }} = 150\)
\(x\left( {\frac{1}{{\tan 52^\circ }} + \frac{1}{{\tan 41^\circ }}} \right) = 150\)
\[x = \frac{{150}}{{\frac{1}{{\tan 52^\circ }} + \frac{1}{{\tan 41^\circ }}}} \approx 78\;\,({\rm{m)}}.\]
Vậy độ cao máy bay là \[78{\rm{ m}}.\]
Đáp án: 78.
Lời giải
Do mặt đất là phương ngang nên \[\widehat {BCA} = 30^\circ \] và \[\widehat {BDA} = 60^\circ \].
Gọi \[x\] (m/phút) là vận tốc xe máy, điều kiện \[x > 0\].
Vì xe máy đi từ \[C\] đến \[D\] trong \[6\] phút nên \[CD = 6x\,\,\left( {\rm{m}} \right)\]
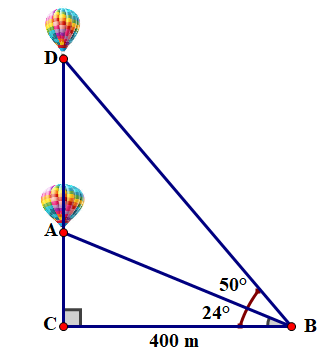
• Xét \[\Delta ABC\] vuông tại \[A\], ta có:
\[AC = AB \cdot \cot \widehat {BCA} = AB \cdot \cot 30^\circ = AB \cdot \tan 60^\circ = \sqrt 3 AB\] (do \[\cot 30^\circ = \tan 60^\circ \]) \[\left( 1 \right)\]
• Xét \[\Delta ABD\] vuông tại \[A\], ta có:
\[AD = AB \cdot \,\cot \widehat {BDA} = AB \cdot \,\cot 60^\circ = AB \cdot \tan 30^\circ = \frac{{\sqrt 3 AB}}{3}\] (do \[\cot 60^\circ = \tan 30^\circ \]) \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[AC - AD = AB\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right)\] nên \[CD = \frac{{2\sqrt 3 }}{3}AB\].
Ta có \[\frac{{AD}}{{CD}} = \frac{{\sqrt 3 AB}}{3}:\frac{{2\sqrt 3 }}{3}AB = \frac{1}{2}\].
Suy ra \[AD = \frac{1}{2}CD = \frac{1}{2} \cdot 6x = 3x\,\,({\rm{m}}).\]
Vậy thời gian để xe máy chạy từ \[D\] đến tòa nhà là \[\frac{{3x}}{x} = 3\] (phút).
Đáp án: 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập