Một khúc sông rộng khoảng \[130\,\,{\rm{m}}\]. Một con đò dự định chèo từ bờ bên này sang bờ bên kia theo phương vuông góc với bờ sông, nhưng do bị dòng nước đẩy xiên nên phải chèo khoảng \[150\,\,{\rm{m}}\] mới sang được bờ bên kia. Dòng nước đã đẩy con đò lệch đi một góc so với phương dự định ban đầu là


Câu hỏi trong đề: Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Chọn A
Tam giác \[ABC\] vuông tại \[B\] có: \[\cos A = \frac{{AB}}{{AC}} = \frac{{130}}{{150}} = \frac{{13}}{{15}}\] nên \[\widehat {BAC} \approx 30^\circ {\rm{.}}\]
Vậy dòng nước đã đẩy con đò lệch đi một góc so với phương dự định ban đầu khoảng \[30^\circ .\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
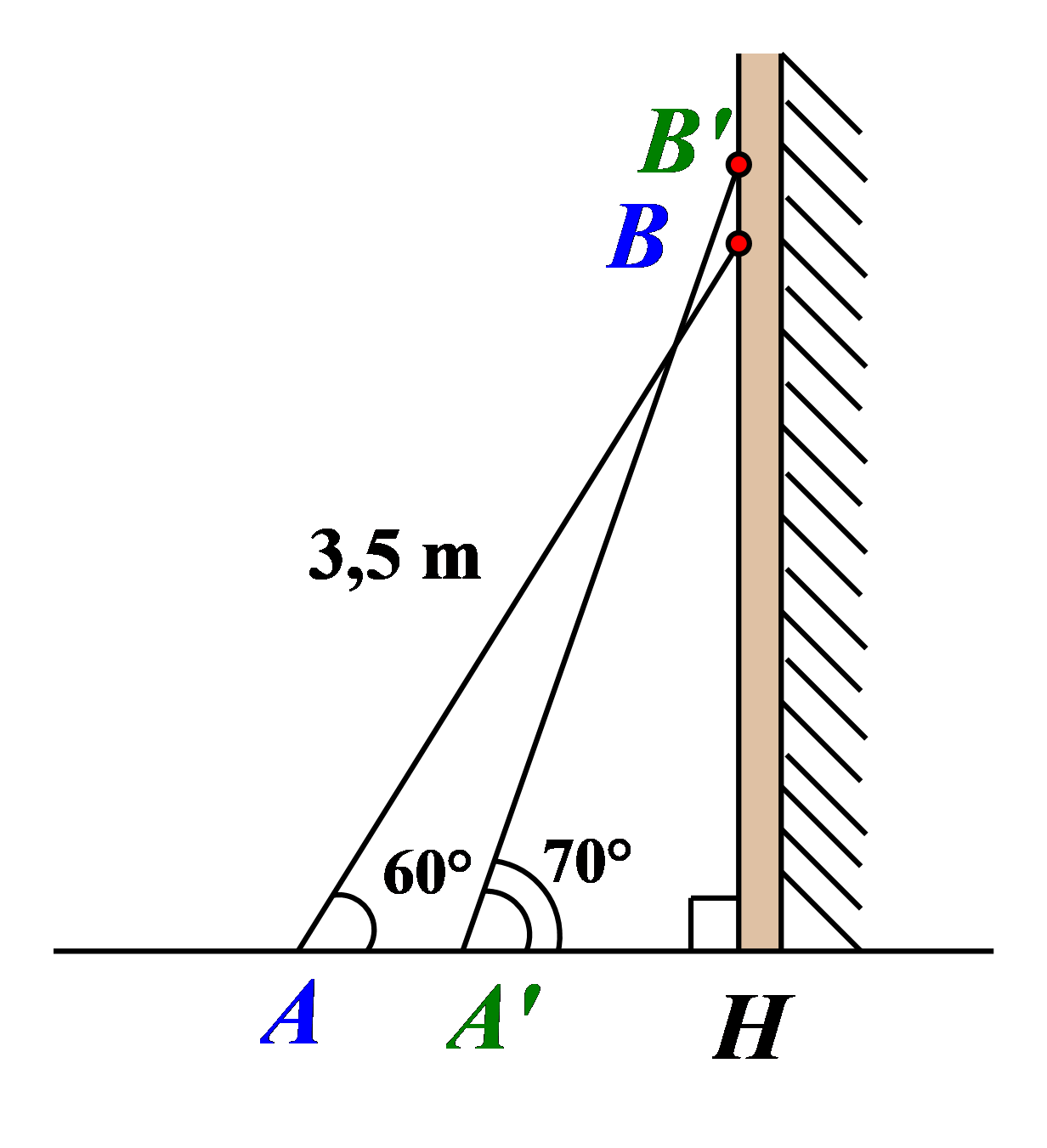
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.
Khi thang tạo với mặt đất một góc có độ lớn \[6{\rm{0}}^\circ \] và \[7{\rm{0}}^\circ \] thì khoảng cách từ chân thang đến chân tường lần lượt là \[AH\] và \[A'H'\].
• Tam giác \[ABH\] vuông tại \[H\] có \[AH = AB \cdot \cos A = 3,5\cos 60^\circ = 1,75\,\,({\rm{m}})\].
• Tam giác \[A'B'H\] vuông tại \[H\] có \[A'H = A'B' \cdot \cos A' = 3,5\cos 70^\circ \approx 1,20\,\,({\rm{m}})\].
Do đó \[1,20\, \le x \le 1,75\].
Lời giải
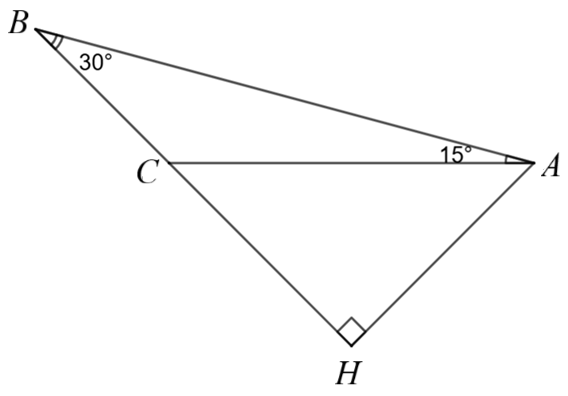
a) Sai. Xét \(\Delta ABC\) có \(\widehat A = 15^\circ \,;\,\,\widehat B = 30^\circ \) nên \(\widehat C = 180^\circ - 15^\circ - 30^\circ = 135^\circ \).
Tam giác \(ABC\) có \(\widehat C\) là góc tù nên tam giác \(ABC\) là tam giác tù.
b) Đúng. Xét \(\Delta HAB\) vuông tại \(H\) có: \(AH = AB \cdot \sin 30^\circ = 7,5\,\,({\rm{cm}}).\)
c) Đúng. Xét \(\Delta HAC\) vuông tại \(H\) có \(\widehat {ACH} = \widehat B + \widehat {CAB} = 45^\circ \) hay \(\Delta HAC\) vuông cân tại \(H.\)
d) Sai. Xét \(\Delta HAB\) vuông tại \(H\) có:\(BH = AB \cdot \cos 30^\circ = \frac{{15\sqrt 3 }}{2}\,\,({\rm{cm}}).\)
Vì \(\Delta HAC\)vuông cân tại \(H\) nên \(CH = 7,5\,\,{\rm{cm}}{\rm{.}}\)
Khi đó, \(BC = BH - CH \approx 5,49\,\,({\rm{cm}}).\)
Vậy \({S_{ABC}} = \frac{1}{2} \cdot AH \cdot BC = \frac{1}{2} \cdot 7,5 \cdot 5,49 = 20,59\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right) \approx 21\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
![a) Độ dài \[AC\] đường dây (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/45-1761183430.png)
![Chọn D Ta có, góc tạo bởi cạnh \[AB\] và phương năm ngang trên mặt đất là \[\widehat {ABH}\]. Xét tam giác \[ABH\] vuôn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/8-1761181578.png)